单选题 (共 10 题 ),每题只有一个选项正确
下列各数中,比﹣2小的数是( )
$\text{A.}$ -3
$\text{B.}$ -1
$\text{C.}$ 0
$\text{D.}$ 2
计算 ( $-a)^{6} \div a^{3}$ 的结果是 ( )
$\text{A.}$ $-a^{3}$
$\text{B.}$ $-a^{2}$
$\text{C.}$ $a^{3}$
$\text{D.}$ $a^{2}$
下面四个几何体中,主视图为三角形的是( )
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为( )
$\text{A.}$ $5.47 \times 10^{8}$
$\text{B.}$ $0.547 \times 10^{8}$
$\text{C.}$ $547 \times 10^{5}$
$\text{D.}$ $5.47 \times 10^{7}$
下列方程中, 有两个相等实数根的是( )
$\text{A.}$ $x^{2}+1=2 x$
$\text{B.}$ $x^{2}+1=0$
$\text{C.}$ $x^{2}-2 x=3$
$\text{D.}$ $x^{2}-2 x=0$
申冉的妈妈在网上销售装饰品. 最近一周, 每天销售某种装饰品的个数为: $11,10,11,13$,
$11,13,15$. 关于这组数据, 冉申得出如下结果, 其中错误的是( )
$\text{A.}$ 众数是 11
$\text{B.}$ 平均数是 12
$\text{C.}$ 方差是 $\frac{18}{7}$
$\text{D.}$ 中位数是 13
已知一次函数 $y=k x+3$ 的图象经过点 $A$, 且 $y$ 随 $x$ 的增大而减小, 则点 $A$ 的坐标可以是 ( )
$\text{A.}$ $(-1,2)$
$\text{B.}$ $(1,-2)$
$\text{C.}$ $(2,3)$
$\text{D.}$ $(3,4)$
如图, Rt $\triangle A B C$ 中, $\angle C=90^{\circ}$, 点 $D$ 在 $A C$ 上, $\angle D B C=\angle A$. 若 $A C=4, \cos A=\frac{4}{5}$, 则 $B D$ 的长度为 ( )
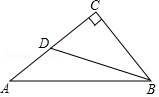
$\text{A.}$ $\frac{9}{4}$
$\text{B.}$ $\frac{12}{5}$
$\text{C.}$ $\frac{15}{4}$
$\text{D.}$ $4$
已知点 $A, B, C$ 在 $\odot O$ 上, 则下列命题为真命题的是 ( )
$\text{A.}$ 若半径 $O B$ 平分弦 $A C$, 则四边形 $O A B C$ 是平行四边形
$\text{B.}$ 若四边形 $O A B C$ 是平行四边形, 则 $\angle A B C=120^{\circ}$
$\text{C.}$ 若 $\angle A B C=120^{\circ}$, 则弦 $A C$ 平分半径 $O B$
$\text{D.}$ 若弦 $A C$ 平分半径 $O B$, 则半径 $O B$ 平分弦 $A C$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
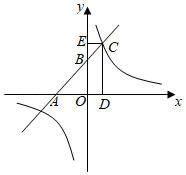
如图, 一次函数 $y=x+k(k>0)$ 的图象与 $x$ 轴和 $y$ 轴分别交于点 $A$ 和点 $B$. 与反比例函数 $y=\frac{k}{x}$ 的图象在第一象限内交于点 $C, C D \perp x$ 轴, $C E \perp y$ 轴. 垂足 分别为点 $D, E$. 当矩形 $O D C E$ 与 $\triangle O A B$ 的面积相等时, $k$ 的值为 ( )
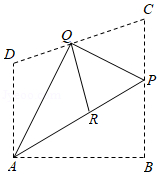
在数学探究活动中, 敏敏进行了如下操作: 如图, 将四边形纸片 $A B C D$ 沿过点 $A$ 的直线折 叠, 使得点 $B$ 落在 $C D$ 上的点 $Q$ 处. 折痕为 $A P$; 再将 $\triangle P C Q, \triangle A D Q$ 分别沿 $P Q, A Q$ 折叠, 此时点 $C, D$ 落在 $A P$ 上的同一点 $R$ 处. 请完成下列探究:
(1) $\angle P A Q$ 的大小为 ( )
(2) 当四边形 $A P C D$ 是平行四边形时, $\frac{A B}{O R}$ 的值为 ( )
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式: $\frac{2 x-1}{2}>1$.
如图, 在由边长为 1 个单位长度的小正方形组成的网格中, 给出了以格点 (网格线的交点) 为端点的线段 $A B$, 线段 $M N$ 在网格线上.
(1) 画出线段 $A B$ 关于线段 $M N$ 所在直线对称的线段 $A_{1} B_{1}$ (点 $A_{1}, B_{1}$ 分别为 $A, B$ 的对 应点);
(2) 将线段 $B_{1} A_{1}$ 绕点 $B_{1}$ 顺时针旋转 $90^{\circ}$ 得到线段 $B_{1} A_{2}$, 画出线段 $B_{1} A_{2}$.
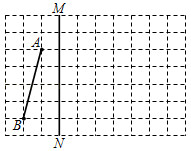
观察以下等式:
第 1 个等式: $\frac{1}{3} \times\left(1+\frac{2}{1}\right)=2-\frac{1}{1}$,
第 2 个等式: $\frac{3}{4} \times\left(1+\frac{2}{2}\right)=2-\frac{1}{2}$,
第 3 个等式: $\frac{5}{5} \times\left(1+\frac{2}{3}\right)=2-\frac{1}{3}$,
第 4 个等式: $\frac{7}{6} \times\left(1+\frac{2}{4}\right)=2-\frac{1}{4}$.
第 5 个等式: $\frac{9}{7} \times\left(1+\frac{2}{5}\right)=2-\frac{1}{5}$.
$\cdots$
按照以上规律, 解决下列问题:
(1) 写出第 6 个等式: $\frac{11}{8} \times\left(1+\frac{2}{6}\right)=2-\frac{1}{6}$;
(2)写出你猜想的第 $n$ 个等式: $\frac{2 n-1}{n+2} \times\left(1+\frac{2}{n}\right)=2-\frac{1}{n}$ (用含 $n$ 的等式表示), 并 证明.
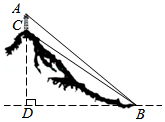
如图, 山顶上有一个信号塔 $A C$, 已知信号塔高 $A C=15$ 米, 在山脚下点 $B$ 处测得塔底 $C$ 的 仰角 $\angle C B D=36.9^{\circ}$, 塔顶 $A$ 的仰角 $\angle A B D=42.0^{\circ}$, 求山高 $C D$ (点 $A, C, D$ 在同一条 坚直线上).
(参考数据: $\tan 36.9^{\circ} \approx 0.75, \sin 36.9^{\circ} \approx 0.60, \tan 42.0^{\circ} \approx 0.90 .$ )
某超市有线上和线下两种销售方式. 与 2019 年 4 月份相比, 该超市 2020 年 4 月份销售总 额增长 $10 \%$, 其中线上销售额增长 $43 \%$, 线下销售额增长 4\%.
(1)设 2019 年 4 月份的销售总额为 $a$ 元, 线上销售额为 $x$ 元, 请用含 $a, x$ 的代数式表 示 2020 年 4 月份的线下销售额(直接在表格中填写结果);

(2) 求 2020 年 4 月份线上销售额与当月销售总额的比值.
如图, $A B$ 是半圆 $O$ 的直径, $C, D$ 是半圆 $O$ 上不同于 $A, B$ 的两点, $A D=B C, A C$ 与 $B D$ 相交于点 $F . B E$ 是半圆 $O$ 所在圆的切线, 与 $A C$ 的延长线相交于点 $E$.
(1) 求证: $\triangle C B A \cong \triangle D A B$;
(2) 若 $B E=B F$, 求证: $A C$ 平分 $\angle D A B$.

某单位食堂为全体 960 名职工提供了 $A, B, C, D$ 四种套餐, 为了解职工对这四种套餐的 喜好情况, 单位随机抽取 240 名职工进行 “你最喜欢哪一种套餐 (必选且只选一种)” 问 卷调查. 根据调查结果绘制了条形统计图和扇形统计图, 部分信息如下:
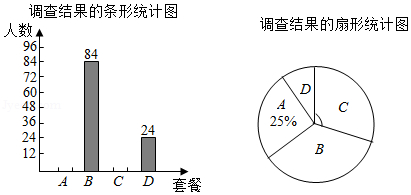
(1) 在抽取的 240 人中最喜欢 $A$ 套餐的人数为
扇形统计图中 “ $C$ ” 对应扇形的圆 心角的大小为
(2) 依据本次调查的结果, 估计全体 960 名职工中最喜欢 $B$ 套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任 “食品安全监督员”, 求甲被选到的 概率.
在平面直角坐标系中, 已知点 $A(1,2), B(2,3), C(2,1)$, 直线 $y=x+m$ 经过点 $A$, 抛物线 $y=a x^{2}+b x+1$ 恰好经过 $A, B, C$ 三点中的两点.
(1) 判断点 $B$ 是否在直线 $y=x+m$ 上, 并说明理由;
(2) 求 $a, b$ 的值;
(3) 平移抛物线 $y=a x^{2}+b x+1$, 使其顶点仍在直线 $y=x+m$ 上, 求平移后所得抛物线与 $y$ 轴交点纵坐标的最大值.
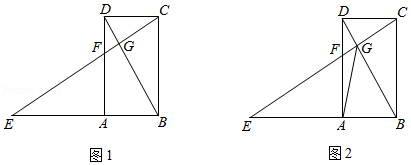
如图 1, 已知四边形 $A B C D$ 是矩形, 点 $E$ 在 $B A$ 的延长线上, $A E=A D$. $E C$ 与 $B D$ 相交于点
$G$, 与 $A D$ 相交于点 $F, A F=A B$.
(1) 求证: $B D \perp E C$;
(2)若 $A B=1$, 求 $A E$ 的长;
(3) 如图 2, 连接 $A G$, 求证: $E G-D G=\sqrt{2} A G$.