单选题 （共 8 题 ），每题只有一个选项正确
下面用数学家名字命名的图形中，既是轴对称图形，又是中心对称图形的是
$\text{A.}$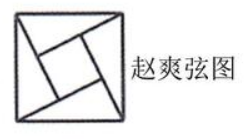 
$\text{B.}$ 
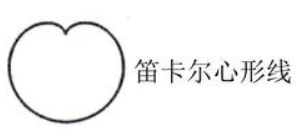$\text{C.}$ 
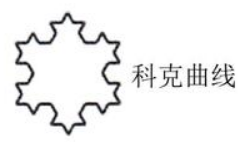$\text{D.}$ 
根据等式的性质, 下列各式变形正确的是
$\text{A.}$ 若 $\frac{a}{c}=\frac{b}{c}$ ，则 $\mathrm{a}=\mathrm{b}$
$\text{B.}$ 若 $a c=b c$, 则 $a=b$
$\text{C.}$ 若 $a^2=b^2$, 则 $a=b$
$\text{D.}$ 若 $-\frac{1}{3} x=6$, 则 $x=-2$
下列运算正确的是
$\text{A.}$ $3 x^2+4 x^3=7 x^5$
$\text{B.}$ $(x+y)^2=x^2+y^2$
$\text{C.}$ $(2+3 x)(2-3 x)=9 x^2-4$
$\text{D.}$ $2 x y+4 x y^2=2 x y(1+2 y)$
已知关于 $x$ 的方程 $x^2+m x+3=0$ 的一个根为 $x=1$, 则实数 $m$ 的值为
$\text{A.}$ 4
$\text{B.}$ -4
$\text{C.}$ 3
$\text{D.}$ -3
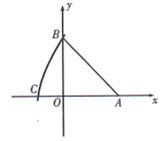
如图 1 所示, $A(2 \sqrt{2}, 0), A B=3 \sqrt{2}$, 以点 $A$ 为圆心, $A B$ 长为半径画弧交 $x$ 轴 负半轴于点 $C$, 则点 $C$ 的坐标为
$\text{A.}$ $(3 \sqrt{2}, 0)$
$\text{B.}$ $(\sqrt{2}, 0)$
$\text{C.}$ $(-\sqrt{2}, 0)$
$\text{D.}$ $(-3 \sqrt{2}, 0)$
数学课上老师用双手形象的表示了 “三线八角” 图形, 如图 2 所示 (两大拇指 代表被截直线, 食指代表截线). 从左至右依次表示
$\text{A.}$ 同旁内角、同位角、内错角
$\text{B.}$ 同位角、内错角、对顶角
$\text{C.}$ 对顶角、同位角、同旁内角
$\text{D.}$ 同位角、内错角、同旁内角
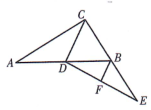
如图 3, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, D$ 是 $A B$ 的中点, 延长 $C B$ 至点 $E$, 使 $B E=B C$,
连接 $D E, F$ 为 $D E$ 中点, 连接 $B F$. 若 $A C=16, B C=12$, 则 $B F$ 的长为
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
2022 年 2 月 5 日, 电影 《长津湖》在青海剧场首映, 小李一家开车去观看.最 初以某一速度匀速行驶, 中途停车加油耽误了十几分钟, 为了按时到达剧场, 小李在不违反交通规则的前提下加快了速度, 仍保持匀速行驶. 在此行驶过程中, 汽车离剧场的距离 $\mathrm{y}$ (千米)与行驶时间 $\mathrm{t}$ (小时)的函数关系的大致图象是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$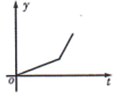 
$\text{D.}$ 
填空题 （共 18 题 ），请把答案直接填写在答题纸上
若式子 $\frac{1}{\sqrt{x-1}}$ 有意义, 则实数 $\mathrm{x}$ 的取值范围是
习近平总书记指出 “善于学习, 就是善于进步” , “学习强国” 平台上线的某 天, 全国大约有 124600000 人在平台上学习, 将这个数据用科学记数法表示 为
不等式组 $\left\{\begin{array}{c}2 x+4 \geq 0 \\ 6-x>3\end{array}\right.$ 的所有整数解的和为
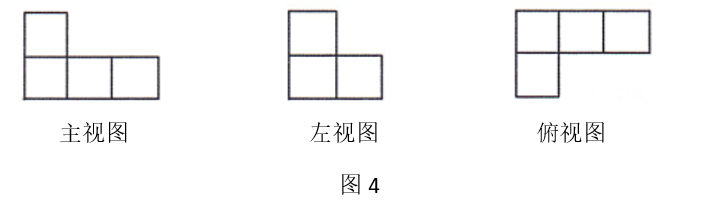
由若干个相同的小正方体构成的几何体的三视图如图 4 所示, 那么构成这个 几何体的小正方体的个数是
如图 5, 一块砖的 A, B, C三个面的面积之比是 5: 3: 1. 如果 A, B, C三个 面分别向下在地上, 地面所受压强分别为 $P_1, P_2, P_3$, 压强的计算公式为 $P=\frac{F}{\mathrm{~s}}$, , 其中 $P$ 是压强, $F$ 是压力, $S$ 是受力面积, 则 $P_1, P_2, P_3$ 的大小关系为 (用小于号连接).
如图 6, 在 Rt $\triangle A B C$ 中, $\angle A B C=90^{\circ}, E D$ 是 $A C$ 的垂直平分线, 交 $A C$ 于点 $D$, 交 $B C$ 于点 $E, \angle B A E=10^{\circ}$, 则 $\angle C$ 的度数是
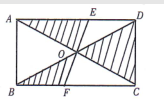
如图 7, 矩形 $A B C D$ 的对角线相交于点 $O$, 过点 $O$ 的直线交 $A D, B C$ 于点 $E 、 F$, 若 $A B=3, B C=4$, 则图中阴影部分的面积为
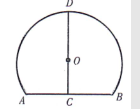
如图 8 是一个隧道的横截面, 它的形状是以点 $\mathrm{O}$ 为圆心的圆的一部分, 如果 $C$ 是 $\odot O$ 中弦 $A B$ 的中点, $C D$ 经过圆心 $O$ 交 $\odot O$ 于点 $D$, 并且 $A B=4 m, C D=6 m$, 则$\odot O$ 的半径长为 $\mathrm{m}$.
如图 9, 从一个腰长为 $60 \mathrm{~cm}$, 顶角为 $120^{\circ}$ 的等腰三角形铁皮 $O A B$ 中剪出一个最大的扇形 OCD, 则此扇形的弧长为 $\mathrm{cm}$.
如图 10 , 小明同学用一张长 $11 \mathrm{~cm}$, 宽 $7 \mathrm{~cm}$ 的矩形纸板制作一个底面积为 $21 \mathrm{~cm}^2$ 的无盖长方体纸盒, 他将纸板的四个角各剪去一个同样大小的正方形, 将四周向上折叠即可(损耗不计). 设剪去的正方形边长为 $\mathrm{xcm}$, 则可列出关于 $\mathrm{x}$ 的方程为
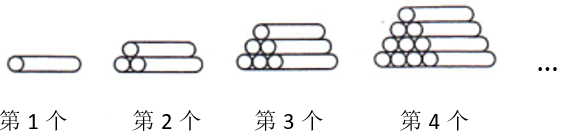
木材加工厂将一批木料按如图 11 所示的规律依次摆放, 则第 $n$ 个图中共有木料 （ ） 根.
解方程: $\frac{x}{x-2}-1=\frac{4}{x^2-4 x+4}$
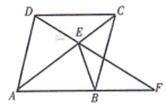
如图 12, 四边形 $A B C D$ 为菱形, $E$ 为对角线 $A C$ 上的一个动点(不与点 $A$, $C$ 重合), 连接 $D E$ 并延长交射线 $A B$ 于点 $F$, 连接 $B E$.
(1)求证: $\triangle \mathrm{DCE} \cong \triangle B C E$;
(2)求证: $\angle \mathrm{AFD}=\angle \mathrm{EBC}$.
随着我国科学技术的不断发展, 科学幻想变为现实.如图 13-1 是我国自 主研发的某型号隐形战斗机模型, 全动型后掠翼垂尾是这款战斗机亮点之一. 图 13-2 是垂尾模型的轴切面, 并通过垂尾模型的外围测得如下数据, $B C=8, C D=2$, $\angle D=135^{\circ}, \angle C=60^{\circ}$, 且 $A B / / C D$, 求出垂尾模型 $A B C D$ 的面积.(结果保留整数, 参考数据: $\sqrt{2} \approx 1.414, \quad \sqrt{3} \approx 1.732)$
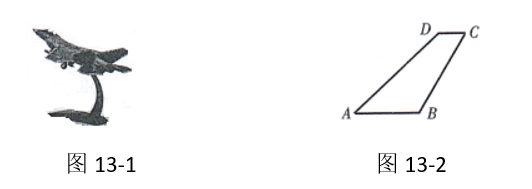
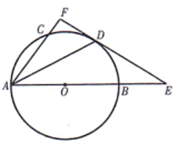
如图 14, $A B$ 是 $\odot O$ 的直径, $A C$ 是 $\odot O$ 的弦, $A D$ 平分 $\angle C A B$ 交 $\odot O$ 于 点 $D$, 过点 $D$ 作 $\odot O$ 的切线 $E F$, 交 $A B$ 的延长线于点 $E$, 交 $A C$ 的延长线于点
$\mathrm{F}$
(1)求证: $A F \perp E F$;
(2) 若 $C F=1, A C=2, A B=4$, 求 $B E$ 的长.
)为迎接党的二十大胜利召开, 某校对七、八年级的学生进行了党史学 习宣传教育, 其中七、八年级的学生各有 500 人. 为了解该校七、八年级学生 对党史知识的掌握情况, 从七、八年级学生中各随机抽取 15 人进行党史知识 测试, 统计这部分学生的测试成绩(成绩均为整数, 满分 10 分, 8 分及 8 分以 上为优秀), 相关数据统计、整理如下:
七年级抽取学生的成绩: $6,6,6,8,8,8,8,8,8,8,9,9,9,10$.
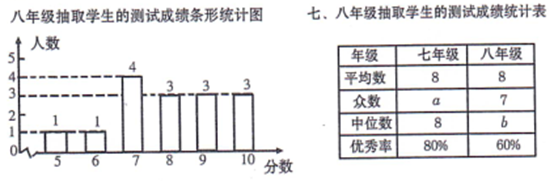
(1)填空:a= , $b=$
(2)根据以上数据, 你认为该校七、八年级中, 哪个年级的学生党史知识掌握得 较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得 10 分的 4 名学生中随机抽取 2 人参加党史知识竞赛, 请用列表法或画树状图法, 求出被选中的 2 人恰好是七、八年级各 1 人的概 率.
两个顶角相等的等腰三角形, 如果具有公共的顶角的顶点, 并把它们 的底角顶点连接起来, 则形成一组全等的三角形, 把具有这个规律的图形称 为 “手拉手” 图形.
(1)问题发现:
如图 15-1, 若 $\triangle A B C$ 和 $\triangle A D E$ 是顶角相等的等腰三角形, $B C, D E$ 分别是 底边. 求证: $B D=C E$;
(2)解决问题:
如图 15-2, 若 $\triangle \mathrm{ACB}$ 和 $\triangle \mathrm{DCE}$ 均为等腰直角三角形, $\angle \mathrm{ACB}=\angle \mathrm{DCE}=90^{\circ}$, 点 $A, D, E$ 在同一条直线上, $C M$ 为 $\triangle D C E$ 中 $D E$ 边上的高, 连接 $B E$, 请判断 $\angle \mathrm{AEB}$ 的度数及线段 $\mathrm{CM}, \mathrm{AE}, \mathrm{BE}$ 之间的数量关系并说明理由.
解答题 （共 1 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
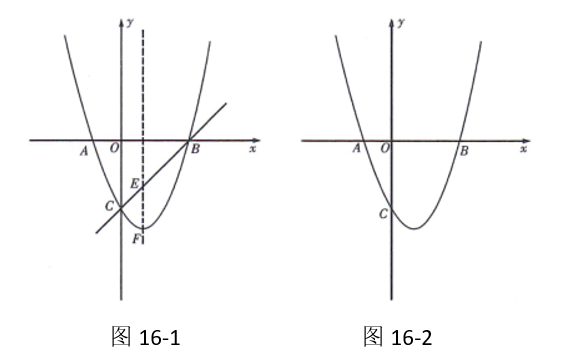
如图 16-1, 抛物线 $y=x^2+b x+c$ 与 $x$ 轴交于 $A(-1,0), B(3,0)$ 两点, 与 $y$ 轴交于 点 $C$.
(1)求该抛物线的解析式;
(2)若点 $E$ 是抛物线的对称轴与直线 $B C$ 的交点, 点 $F$ 是抛物线的顶点, 求 $E F$ 的长;
(3)设点 $P$ 是(1)中抛物线上的一个动点, 是否存在满足 $\mathrm{S}_{\triangle \mathrm{PAB}}=6$ 的点 $P$ ?如果存 在, 请求出点 P的坐标; 若不存在, 请说明理由.(请在图 16-2 中探讨)
