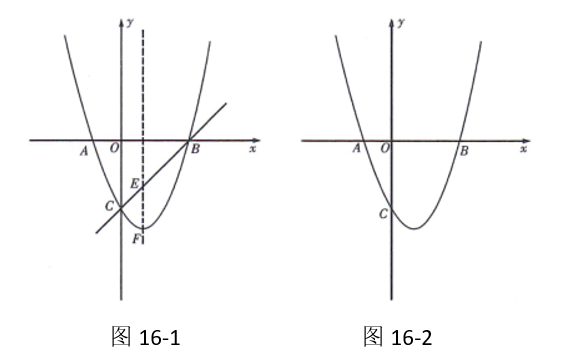
如图 16-1, 抛物线 $y=x^2+b x+c$ 与 $x$ 轴交于 $A(-1,0), B(3,0)$ 两点, 与 $y$ 轴交于 点 $C$.
(1)求该抛物线的解析式;
(2)若点 $E$ 是抛物线的对称轴与直线 $B C$ 的交点, 点 $F$ 是抛物线的顶点, 求 $E F$ 的长;
(3)设点 $P$ 是(1)中抛物线上的一个动点, 是否存在满足 $\mathrm{S}_{\triangle \mathrm{PAB}}=6$ 的点 $P$ ?如果存 在, 请求出点 P的坐标; 若不存在, 请说明理由.(请在图 16-2 中探讨)