)为迎接党的二十大胜利召开, 某校对七、八年级的学生进行了党史学 习宣传教育, 其中七、八年级的学生各有 500 人. 为了解该校七、八年级学生 对党史知识的掌握情况, 从七、八年级学生中各随机抽取 15 人进行党史知识 测试, 统计这部分学生的测试成绩(成绩均为整数, 满分 10 分, 8 分及 8 分以 上为优秀), 相关数据统计、整理如下:
七年级抽取学生的成绩: $6,6,6,8,8,8,8,8,8,8,9,9,9,10$.

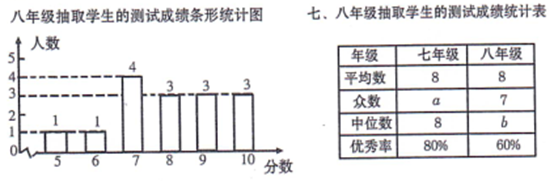
(1)填空:a= , $b=$
(2)根据以上数据, 你认为该校七、八年级中, 哪个年级的学生党史知识掌握得 较好?请说明理由(写出一条即可);
(3)请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;
(4)现从七、八年级获得 10 分的 4 名学生中随机抽取 2 人参加党史知识竞赛, 请用列表法或画树状图法, 求出被选中的 2 人恰好是七、八年级各 1 人的概 率.