解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
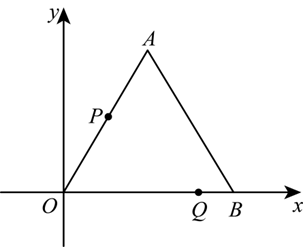
如图,在平面直角坐标系中,等边三角形 $O A B$ 的边 $O B$ 在 $x$ 轴上,点 $A$ 在第一象限,$O A$ 的长度是一元二次方程 $x^2-5 x-6=0$ 的根,动点 $P$ 从点 $O$ 出发以每秒 2 个单位长度的速度沿折线 $O A-A B$ 运动,动点 $Q$从点 $O$ 出发以每秒 3 个单位长度的速度沿折线 $O B-B A$ 运动,$P, ~ Q$ 两点同时出发,相遇时停止运动.设运动时间为 $t$ 秒 $(0 < t < 3.6), \triangle O P Q$ 的面积为 $S$ .
(1)求点 $A$ 的坐标;
(2)求 $S$ 与 $t$ 的函数关系式;
(3)在(2)的条件下,当 $S=6 \sqrt{3}$ 时,点 $M$ 在 $y$ 轴上,坐标平面内是否存在点 $N$ ,使得以点 $O, ~ P, ~ M, ~ N$为顶点的四边形是菱形.若存在,直接写出点 $N$ 的坐标;若不存在,说明理由.
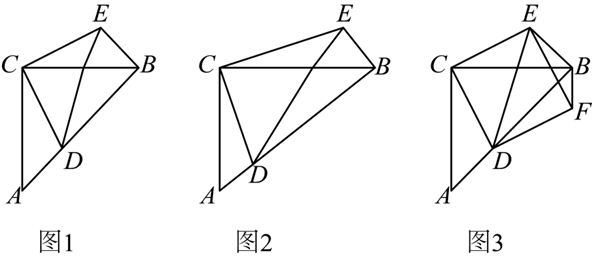
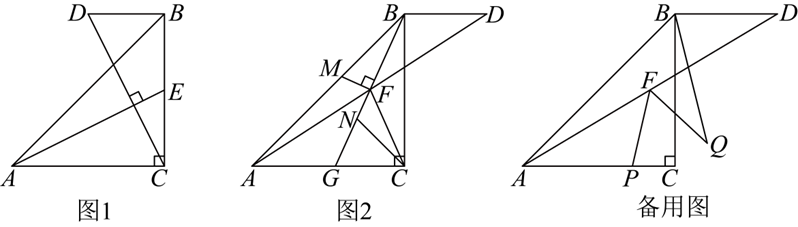
如图,在 Rt $\triangle A B C$ 中,点 $D$ 是斜边 $A B$ 上的动点(点 $D$ 与点 $A$ 不重合),连接 $C D$ ,以 $C D$ 为直角边在 $C D$ 的右侧构造 Rt $\triangle C D E, \angle D C E=90^{\circ}$ ,连接 $B E, \frac{C E}{C D}=\frac{C B}{C A}=m$ .
特例感知
(1)如图 1,当 $m=1$ 时,$B E$ 与 $A D$ 之间的位置关系是 $\qquad$ ,数量关系是 $\qquad$ ;
类比迁移
(2)如图 2,当 $m \neq 1$ 时,猜想 $B E$ 与 $A D$ 之间的位置关系和数量关系,并证明猜想.
拓展应用
(3)在(1)的条件下,点 $F$ 与点 $C$ 关于 $D E$ 对称,连接 $D F, E F, B F$ ,如图 3.已知 $A C=6$ ,设 $A D=x$ ,四边形 $C D F E$ 的面积为 $y$ .
① 求 $y$ 与 $x$ 的函数表达式,并求出 $y$ 的最小值;
② 当 $B F=2$ 时,请直接写出 $A D$ 的长度.
综合与探究:如图,在平面直角坐标系中,已知直线 $y=\frac{1}{2} x-2$ 与 $x$ 轴交于点 $A$ ,与 $y$ 轴交于点 $C$ ,过 $A$ , $C$ 两点的抛物线 $y=a x^2+b x+c(a \neq 0)$ 与 $x$ 轴的另一个交点为点 $B(-1,0)$ ,点 $P$ 是抛物线位于第四象限图象上的动点,过点 $P$ 分别作 $x$ 轴和 $y$ 轴的平行线,分别交直线 $A C$ 于点 $E$ ,点 $F$ .
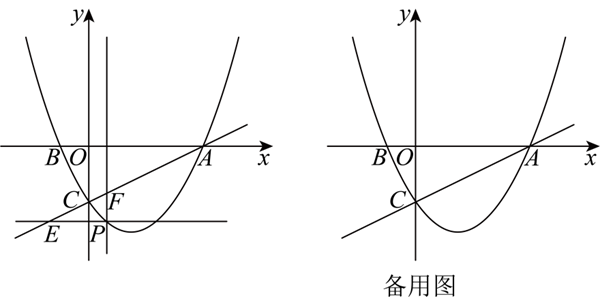
(1)求抛物线的解析式;
(2)点 $D$ 是 $x$ 轴上的任意一点,若 $ A C D$ 是以 $A C$ 为腰的等腰三角形,请直接写出点 $D$ 的坐标;
(3)当 $E F=A C$ 时,求点 $P$ 的坐标;
(4)在(3)的条件下,若点 $N$ 是 $y$ 轴上的一个动点,过点 $N$ 作抛物线对称轴的垂线,垂足为 $M$ ,连接 $N A, M P$ ,则 $N A+M P$ 的最小值为 $\qquad$
在平面直角坐标系 $x O y$ 中,已知抛物线 $F: y=-x^2+b x+c$ 经过点 $A(-3,-1)$ ,与 $y$ 轴交于点 $B(0,2)$ .
(1)求抛物线的函数表达式;
(2)在直线 $A B$ 上方抛物线上有一动点 $C$ ,连接 $O C$ 交 $A B$ 于点 $D$ ,求 $\frac{C D}{O D}$ 的最大值及此时点 $C$ 的坐标;
(3)作抛物线 $F$ 关于直线 $y=-1$ 上一点的对称图象 $F^{\prime}$ ,抛物线 $F$ 与 $F^{\prime}$ 只有一个公共点 $E$(点 $E$ 在 $y$ 轴右侧), $G$ 为直线 $A B$ 上一点,$H$ 为抛物线 $F^{\prime}$ 对称轴上一点,若以 $B, E, G, H$ 为顶点的四边形是平行四边形,求 $G$ 点坐标.
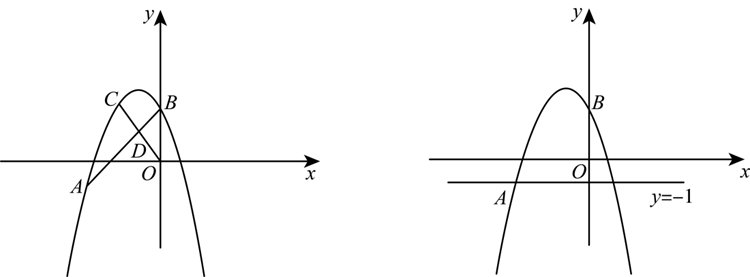
将一个平行四边形纸片 $O A B C$ 放置在平面直角坐标系中,点 $O(0,0)$ ,点 $A(3,0)$ ,点 $B, C$ 在第一象限,且
$$
O C=2, \angle A O C=60^{\circ}
$$

(1)填空:如图(1),点 $C$ 的坐标为 $\qquad$ ,点 $B$ 的坐标为 $\qquad$ ;
(2)若 $P$ 为 $x$ 轴的正半轴上一动点,过点 $P$ 作直线 $l \perp x$ 轴,沿直线 $l$ 折叠该纸片,折叠后点 $O$ 的对应点 $O^{\prime}$ 落在 $x$ 轴的正半轴上,点 $C$ 的对应点为 $C^{\prime}$ .设 $O P=t$ .
(1)如图(2),若直线 $l$ 与边 $C B$ 相交于点 $Q$ ,当折叠后四边形 $P O^{\prime} C^{\prime} Q$ 与 $Y O A B C$ 重叠部分为五边形时,$O^{\prime} C^{\prime}$ 与 $A B$ 相交于点 $E$ .试用含有 $t$ 的式子表示线段 $B E$ 的长,并直接写出 $t$ 的取值范围;
(2)设折叠后重叠部分的面积为 S ,当 $\frac{2}{3} \leq t \leq \frac{11}{4}$ 时,求 S 的取值范围(直接写出结果即可).
已知二次函数 $y=-x^2+c$ 的图像经过点 $A(-2,5)$ ,点 $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$ 是此二次函数的图像上的两个动点.
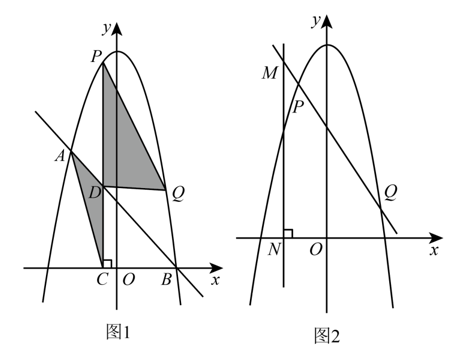
(1)求此二次函数的表达式;
(2)如图 1,此二次函数的图像与 $x$ 轴的正半轴交于点 $B$ ,点 $P$ 在直线 $A B$ 的上方,过点 $P$ 作 $P C \perp x$ 轴于点
$C$ ,交 $A B$ 于点 $D$ ,连接 $A C, D Q, P Q$ .若 $x_2=x_1+3$ ,求证 $\frac{S_{\triangle P D O}}{S_{\triangle A D C}}$ 的值为定值;
(3)如图 2,点 $P$ 在第二象限,$x_2=-2 x_1$ ,若点 $M$ 在直线 $P Q$ 上,且横坐标为 $x_1-1$ ,过点 $M$ 作 $M N \perp x$ 轴于点 $N$ ,求线段 $M N$ 长度的最大值.
【问题背景】
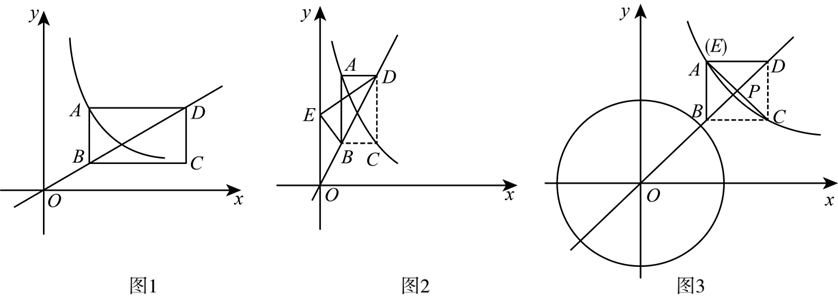
如图 1,在平面直角坐标系中,点 $B, D$ 是直线 $y=a x(a>0)$ 上第一象限内的两个动点 $(O D>O B)$ ,以线段 $B D$ 为对角线作矩形 $A B C D, A D / / x$ 轴.反比例函数 $y=\frac{k}{x}$ 的图象经过点 $A$ .
【构建联系】
(1)求证:函数 $y=\frac{k}{x}$ 的图象必经过点 $C$ .
(2)如图 2,把矩形 $A B C D$ 沿 $B D$ 折叠,点 $C$ 的对应点为 $E$ .当点 $E$ 落在 $y$ 轴上,且点 $B$ 的坐标为 $(1,2)$ 时,求 $k$ 的值.
【深入探究】
(3)如图 3,把矩形 $A B C D$ 沿 $B D$ 折叠,点 $C$ 的对应点为 $E$ .当点 $E$ ,$A$ 重合时,连接 $A C$ 交 $B D$ 于点 $P$ .以点 $O$ 为圆心,$A C$ 长为半径作 e $O$ .若 $O P=3 \sqrt{2}$ ,当 $e O$ 与 $V A B C$ 的边有交点时,求 $k$ 的取值范围.
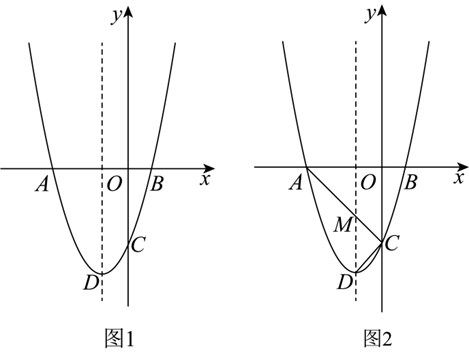
如图 1,抛物线 $y=a x^2+k x-3$ 与 $x$ 轴交于点 $A(-3,0)$ 和点 $B(1,0)$ ,与 $y$ 轴交于点 $C$ .点 $D$ 是抛物线的顶点.
(1)求抛物线的解析式;
(2)如图 2,连接 $A C, D C$ ,直线 $A C$ 交抛物线的对称轴于点 $M$ ,若点 $P$ 是直线 $A C$ 上方抛物线上一点,且 $S_{\triangle P M C}=2 S_{\triangle D M C}$ ,求点 $P$ 的坐标;
(3)若点 $N$ 是抛物线对称轴上位于点 $D$ 上方的一动点,是否存在以点 $N, A, ~ C$ 为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点 $N$ 的坐标;若不存在,请说明理由.
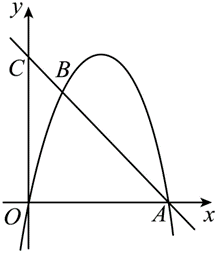
如图,在平面直角坐标系中,二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图像经过原点和点 $A(4,0)$ .经过点 A 的直线与该二次函数图象交于点 $B(1,3)$ ,与 $y$ 轴交于点 $C$ .
(1)求二次函数的解析式及点 $C$ 的坐标;
(2)点 $P$ 是二次函数图象上的一个动点,当点 $P$ 在直线 $A B$ 上方时,过点 $P$ 作 $P E \perp x$ 轴于点 $E$ ,与直线 $A B$ 交于点 $D$ ,设点 $P$ 的横坐标为 $m$ .
① $m$ 为何值时线段 $P D$ 的长度最大,并求出最大值;
② 是否存在点 $P$ ,使得 $\triangle B P D$ 与 $ \triangle A O C$ 相似.若存在,请求出点 $P$ 坐标;若不存在,请说明理由.
如图,抛物线 $y=-\frac{2}{3} x^2+b x+c$ 与 $x$ 轴交于 $A , B$ 两点,与 $y$ 轴交于点 $C$ ,点 A 坐标为 $(-1,0)$ ,点 $B$ 坐标为 $(3,0)$ .
(1)求此抛物线的函数解析式.
(2)点 $P$ 是直线 $B C$ 上方拋物线上一个动点,过点 $P$ 作 $x$ 轴的垂线交直线 $B C$ 于点 $D$ ,过点 $P$ 作 $y$ 轴的垂线,垂足为点 $E$ ,请探究 $2 P D+P E$ 是否有最大值?若有最大值,求出最大值及此时 $P$ 点的坐标;若没有最大值,请说明理由.
(3)点 $M$ 为该抛物线上的点,当 $\angle M C B=45^{\circ}$ 时,请直接写出所有满足条件的点 $M$ 的坐标.
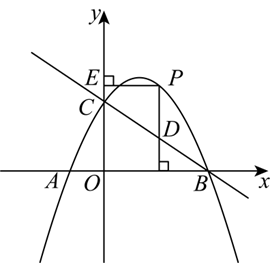
如图,抛物线 $y_1=a x^2+b x+c$ 与 $x$ 轴交于 $A , B$ 两点,与 $y$ 轴交于点 $C, O C=O A, A B=4$ ,对称轴为直线 $l_1: x=-1$ ,将抛物线 $y_1$ 绕点 $O$ 旋转 $180^{\circ}$ 后得到新抛物线 $y_2$ ,抛物线 $y_2$ 与 $y$ 轴交于点 $D$ ,顶点为 $E$ ,对称轴为直线 $l_2$ .
(1)分别求拋物线 $y_1$ 和 $y_2$ 的表达式;
(2)如图1,点 $F$ 的坐标为 $(-6,0)$ ,动点 $M$ 在直线 $l_1$ 上,过点 $M$ 作 $M N / / x$ 轴与直线 $l_2$ 交于点 $N$ ,连接 $F M$ , $D N$ .求 $F M+M N+D N$ 的最小值;
(3)如图 2 ,点 $H$ 的坐标为 $(0,-2)$ ,动点 $P$ 在抛物线 $y_2$ 上,试探究是否存在点 $P$ ,使 $\angle P E H=2 \angle D H E$ ?若存在,请直接写出所有符合条件的点 $P$ 的坐标;若不存在,请说明理由.
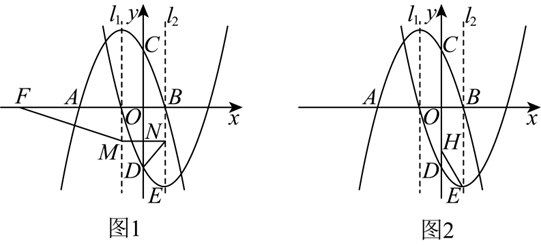
如图 1,抛物线 $y=a(x-h)^2+k$ 交 $x$ 轴于 $O, A(4,0)$ 两点,顶点为 $B(2,2 \sqrt{3})$ .点 $C$ 为 $O B$ 的中点.
(1)求抛物线 $y=a(x-h)^2+k$ 的表达式;
(2)过点 $C$ 作 $C H \perp O A$ ,垂足为 $H$ ,交抛物线于点 $E$ .求线段 $C E$ 的长.
(3)点 $D$ 为线段 $O A$ 上一动点( $O$ 点除外),在 $O C$ 右侧作平行四边形 $O C F D$ .
① 如图 2,当点 $F$ 落在抛物线上时,求点 $F$ 的坐标;
② 如图 3,连接 $B D, B F$ ,求 $B D+B F$ 的最小值.
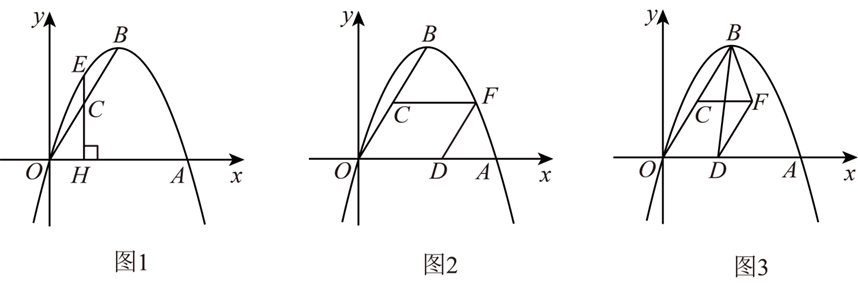
在 Rt $\triangle A B C$ 中,$\angle A C B=90^{\circ}, A C=B C$ ,过点 $B$ 作 $B D / / A C$ .
(1)如图 1,若点 $D$ 在点 $B$ 的左侧,连接 $C D$ ,过点 A 作 $A E \perp C D$ 交 $B C$ 于点 $E$ .若点 $E$ 是 $B C$ 的中点,求证: $A C=2 B D$ ;
(2)如图 2,若点 $D$ 在点 $B$ 的右侧,连接 $A D$ ,点 $F$ 是 $A D$ 的中点,连接 $B F$ 并延长交 $A C$ 于点 $G$ ,连接 $C F$ .过点 $F$ 作 $F M \perp B G$ 交 $A B$ 于点 $M, C N$ 平分 $\angle A C B$ 交 $B G$ 于点 $N$ ,求证:$A M=C N+\frac{\sqrt{2}}{2} B D$ ;
(3)若点 $D$ 在点 $B$ 的右侧,连接 $A D$ ,点 $F$ 是 $A D$ 的中点,且 $A F=A C$ .点 $P$ 是直线 $A C$ 上一动点,连接 $F P$ ,将 $F P$ 绕点 $F$ 逆时针旋转 $60^{\circ}$ 得到 $F Q$ ,连接 $B Q$ ,点 $R$ 是直线 $A D$ 上一动点,连接 $B R, Q R$ .在点 $P$ 的运动过程中,当 $B Q$ 取得最小值时,在平面内将 $V B Q R$ 沿直线 $Q R$ 翻折得到 $\triangle T Q R$ ,连接 $F T$ .在点 $R$ 的运动过程中,直接写出 $\frac{F T}{C P}$ 的最大值.