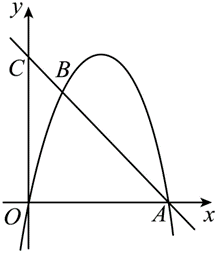
如图，在平面直角坐标系中，二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图像经过原点和点 $A(4,0)$ ．经过点 A 的直线与该二次函数图象交于点 $B(1,3)$ ，与 $y$ 轴交于点 $C$ ．
（1）求二次函数的解析式及点 $C$ 的坐标；
（2）点 $P$ 是二次函数图象上的一个动点，当点 $P$ 在直线 $A B$ 上方时，过点 $P$ 作 $P E \perp x$ 轴于点 $E$ ，与直线 $A B$ 交于点 $D$ ，设点 $P$ 的横坐标为 $m$ ．
① $m$ 为何值时线段 $P D$ 的长度最大，并求出最大值；
② 是否存在点 $P$ ，使得 $\triangle B P D$ 与 $ \triangle A O C$ 相似．若存在，请求出点 $P$ 坐标；若不存在，请说明理由．