【问题背景】
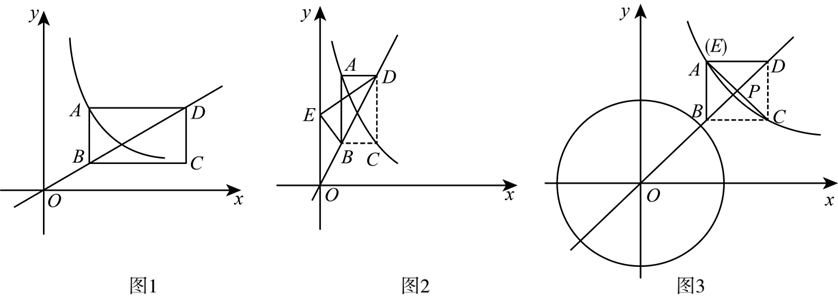
如图 1，在平面直角坐标系中，点 $B, D$ 是直线 $y=a x(a>0)$ 上第一象限内的两个动点 $(O D>O B)$ ，以线段 $B D$ 为对角线作矩形 $A B C D, A D / / x$ 轴．反比例函数 $y=\frac{k}{x}$ 的图象经过点 $A$ ．
【构建联系】
（1）求证：函数 $y=\frac{k}{x}$ 的图象必经过点 $C$ ．
（2）如图 2，把矩形 $A B C D$ 沿 $B D$ 折叠，点 $C$ 的对应点为 $E$ ．当点 $E$ 落在 $y$ 轴上，且点 $B$ 的坐标为 $(1,2)$ 时，求 $k$ 的值．

【深入探究】
（3）如图 3，把矩形 $A B C D$ 沿 $B D$ 折叠，点 $C$ 的对应点为 $E$ ．当点 $E$ ，$A$ 重合时，连接 $A C$ 交 $B D$ 于点 $P$ ．以点 $O$ 为圆心，$A C$ 长为半径作 e $O$ ．若 $O P=3 \sqrt{2}$ ，当 $e O$ 与 $V A B C$ 的边有交点时，求 $k$ 的取值范围．