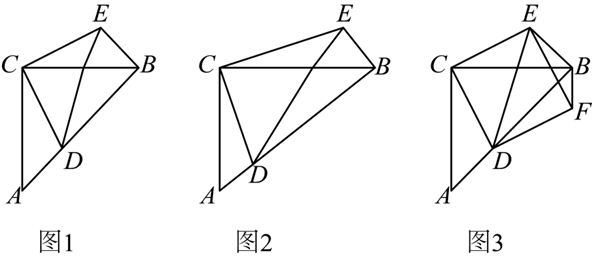
如图，在 Rt $\triangle A B C$ 中，点 $D$ 是斜边 $A B$ 上的动点（点 $D$ 与点 $A$ 不重合），连接 $C D$ ，以 $C D$ 为直角边在 $C D$ 的右侧构造 Rt $\triangle C D E, \angle D C E=90^{\circ}$ ，连接 $B E, \frac{C E}{C D}=\frac{C B}{C A}=m$ ．



特例感知
（1）如图 1，当 $m=1$ 时，$B E$ 与 $A D$ 之间的位置关系是 $\qquad$ ，数量关系是 $\qquad$ ；

类比迁移
（2）如图 2，当 $m \neq 1$ 时，猜想 $B E$ 与 $A D$ 之间的位置关系和数量关系，并证明猜想．
拓展应用
（3）在（1）的条件下，点 $F$ 与点 $C$ 关于 $D E$ 对称，连接 $D F, E F, B F$ ，如图 3．已知 $A C=6$ ，设 $A D=x$ ，四边形 $C D F E$ 的面积为 $y$ ．
① 求 $y$ 与 $x$ 的函数表达式，并求出 $y$ 的最小值；
② 当 $B F=2$ 时，请直接写出 $A D$ 的长度．