已知二次函数 $y=-x^2+c$ 的图像经过点 $A(-2,5)$ ，点 $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$ 是此二次函数的图像上的两个动点．


（1）求此二次函数的表达式；
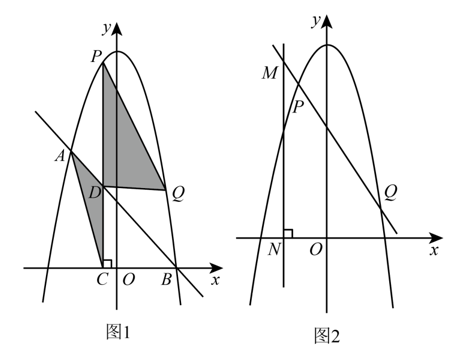
（2）如图 1，此二次函数的图像与 $x$ 轴的正半轴交于点 $B$ ，点 $P$ 在直线 $A B$ 的上方，过点 $P$ 作 $P C \perp x$ 轴于点
$C$ ，交 $A B$ 于点 $D$ ，连接 $A C, D Q, P Q$ ．若 $x_2=x_1+3$ ，求证 $\frac{S_{\triangle P D O}}{S_{\triangle A D C}}$ 的值为定值；
（3）如图 2，点 $P$ 在第二象限，$x_2=-2 x_1$ ，若点 $M$ 在直线 $P Q$ 上，且横坐标为 $x_1-1$ ，过点 $M$ 作 $M N \perp x$ 轴于点 $N$ ，求线段 $M N$ 长度的最大值．