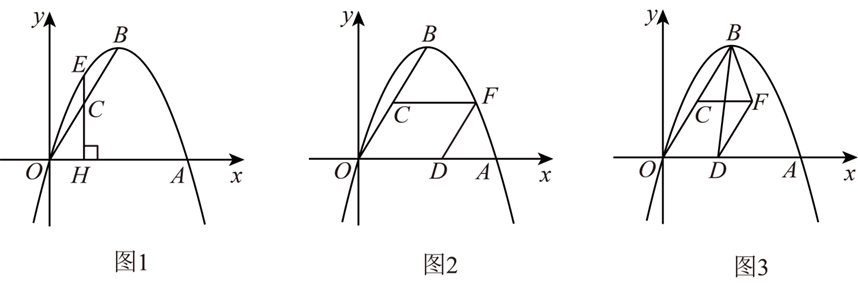
如图 1，抛物线 $y=a(x-h)^2+k$ 交 $x$ 轴于 $O, A(4,0)$ 两点，顶点为 $B(2,2 \sqrt{3})$ ．点 $C$ 为 $O B$ 的中点．
（1）求抛物线 $y=a(x-h)^2+k$ 的表达式；
（2）过点 $C$ 作 $C H \perp O A$ ，垂足为 $H$ ，交抛物线于点 $E$ ．求线段 $C E$ 的长．
（3）点 $D$ 为线段 $O A$ 上一动点（ $O$ 点除外），在 $O C$ 右侧作平行四边形 $O C F D$ ．
① 如图 2，当点 $F$ 落在抛物线上时，求点 $F$ 的坐标；
② 如图 3，连接 $B D, B F$ ，求 $B D+B F$ 的最小值．
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$
$\text{E.}$
$\text{F.}$