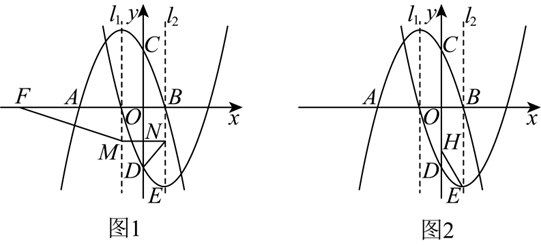
如图，抛物线 $y_1=a x^2+b x+c$ 与 $x$ 轴交于 $A , B$ 两点，与 $y$ 轴交于点 $C, O C=O A, A B=4$ ，对称轴为直线 $l_1: x=-1$ ，将抛物线 $y_1$ 绕点 $O$ 旋转 $180^{\circ}$ 后得到新抛物线 $y_2$ ，抛物线 $y_2$ 与 $y$ 轴交于点 $D$ ，顶点为 $E$ ，对称轴为直线 $l_2$ ．



（1）分别求拋物线 $y_1$ 和 $y_2$ 的表达式；
（2）如图1，点 $F$ 的坐标为 $(-6,0)$ ，动点 $M$ 在直线 $l_1$ 上，过点 $M$ 作 $M N / / x$ 轴与直线 $l_2$ 交于点 $N$ ，连接 $F M$ ， $D N$ ．求 $F M+M N+D N$ 的最小值；
（3）如图 2 ，点 $H$ 的坐标为 $(0,-2)$ ，动点 $P$ 在抛物线 $y_2$ 上，试探究是否存在点 $P$ ，使 $\angle P E H=2 \angle D H E$ ？若存在，请直接写出所有符合条件的点 $P$ 的坐标；若不存在，请说明理由．