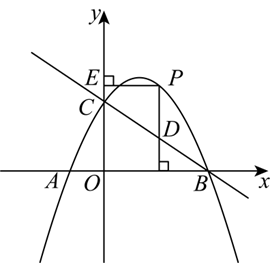
如图，抛物线 $y=-\frac{2}{3} x^2+b x+c$ 与 $x$ 轴交于 $A , B$ 两点，与 $y$ 轴交于点 $C$ ，点 A 坐标为 $(-1,0)$ ，点 $B$ 坐标为 $(3,0)$ ．
（1）求此抛物线的函数解析式．
（2）点 $P$ 是直线 $B C$ 上方拋物线上一个动点，过点 $P$ 作 $x$ 轴的垂线交直线 $B C$ 于点 $D$ ，过点 $P$ 作 $y$ 轴的垂线，垂足为点 $E$ ，请探究 $2 P D+P E$ 是否有最大值？若有最大值，求出最大值及此时 $P$ 点的坐标；若没有最大值，请说明理由．
（3）点 $M$ 为该抛物线上的点，当 $\angle M C B=45^{\circ}$ 时，请直接写出所有满足条件的点 $M$ 的坐标．