解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 的对边分别为 $a, b, c$. 已知 $a=\sqrt{6}, b=2 c, \cos A=-\frac{1}{4}$.
(1)求 $c$ 的值;
(2)求 $\sin B$ 的值;
(3)求 $\sin (2 A-B)$ 的值.
如图, 在圆内接四边形 $A B C D$ 中, $\angle B=120^{\circ}, A B=2, A D=2 \sqrt{2}, \triangle A B C$ 的面积为 $\sqrt{3}$.
(1)求 $A C$;
(2)求 $\angle A C D$.
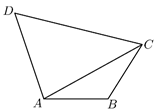
在锐角 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $c-2 b \cos A=b$.
(1)求证: $A=2 B$;
(2)若 $A$ 的角平分线交 $B C$ 于 $D$, 且 $c=2$, 求 $\triangle A B D$ 面积的取值范围.
已知等比数列 $\left\{a_n\right\}$ 的各项均为正数, 其前 $n$ 项和为 $S_n$, 且 $3 a_1, a_3, 5 a_2$ 成等差数列, $S_4+5=5 a_3$.
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=a_n \cdot \log _3 a_{n+1}$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
设数列 $\left\{a_n\right\}$ 满足 $a_1+3 a_2+\cdots+(2 n-1) a_n=2 n$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 求数列 $\left\{\frac{a_n}{2 n+1}\right\}$ 的前 $n$ 项和.
在数列 $\left\{a_n\right\}$ 中, $a_1=-1, a_n=2 a_{n-1}+3 n-6\left(n \geq 2, n \in N^*\right)$.
(1)求证: 数列 $\left\{a_n+3 n\right\}$ 为等比数列, 并求数列 $\left\{a_n\right\}$ 的通项公式;
(2)设 $b_n=a_n+n$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
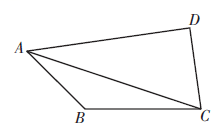
如图, 在平面四边形 $A B C D$ 中, 对角线 $A C$ 平分 $\angle B A D, \triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $\sqrt{2} b \cos B+$ $a \cos C+c \cos A=0$
(1)求 $B$;
(2)若 $A B=C D=2, \triangle A B C$ 的面积为 2 , 求 $A D$
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别 $a, b, c$, 且 $b \cos A+a \cos B=2 c \cos A$
(1)求角 $A$ 的值;
(2)已知 $D$ 在边 $B C$ 上, 且 $B D=3 D C, A D=3$, 求 $\triangle A B C$ 的面积的最大值.
在锐角 $\triangle A B C$ 中, 角 $A, B, C$, 的对边分别为 $a, b, c$, 从条件(1): $\sin A \cos A \tan A=\frac{3}{4}$, 条件(2): $\frac{\sqrt{3} \sin A-\cos A}{\sqrt{3} \sin A+\cos A}=\frac{1}{2}$, 条件(3): $2 a \cos A-b \cos C=c \cos B$ 这三个条件中选择一个作为已知条件.
(1)求角 $A$ 的大小;
(2)若 $a=2$, 求 $\triangle A B C$ 周长的取值范围.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_n=2 a_n+2 n-5$.
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2)记 $b_n=\log _2\left(a_{n+1}-2\right)$, 求数列 $\left\{\frac{1}{b_n \cdot b_{n+1}}\right\}$ 的前 $n$ 项和 $T_n$.
已知 $\left\{a_n\right\}$ 是等差数列, $\left\{b_n\right\}$ 是等比数列, 且 $b_2=3, b_3=9, a_1=b_1, a_{14}=b_4$.
(1)求 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $c_n=a_n+(-1)^n b_n\left(n \in N^*\right)$, 求数列 $\left\{c_n\right\}$ 的前 $2 n$ 项和.
设数列 $\left\{a_n\right\}$ 满足 $a_1=2, a_n-2 a_{n-1}=2-n(n \in N *)$.
(1)求证: $\left\{a_n-n\right\}$ 为等比数列, 并求 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=\left(a_n-n\right) \cdot n$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.