单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\{4,5,6,8\}, B=\{3,5,7,8\}$, 则 $A \cap B=$()
$\text{A.}$ $\{3,5\}$
$\text{B.}$ $\{6,8\}$
$\text{C.}$ $\{5,8\}$
$\text{D.}$ $\{3,4,5,6,7,8\}$
2. 下列对应关系:
(1) $A=\{1,4,9\}, B=\{-3,-2,-1,1,2,3\}, f: x \rightarrow \sqrt{x}$
(2) $A=R, B=R, f: x \rightarrow \frac{1}{x}$
(3) $A=R, B=R, f: x \rightarrow x^2-2$
(4) $A=\{-1,0,1\}, B=\{-1,0,1\}, f:A$中的平方数
其中是 $A$ 到 $B$ 的映射的是 ( )
$\text{A.}$ (1) (3)
$\text{B.}$ (2) (4)
$\text{C.}$ (3) (4)
$\text{D.}$ (2) (3)
下列函数中与函数 $y=x$ 相同的是()
$\text{A.}$ $y=\sqrt[3]{x^3}$
$\text{B.}$ $y=\frac{x^2}{x}$
$\text{C.}$ $y=\sqrt{x^2}$
$\text{D.}$ $y=i$
函数 $f(x)=\sqrt{x+3}+\frac{1}{x+2}$ 的定义域为 $($ )
$\text{A.}$ $(-3,-2) \cup(-2,+\infty)$
$\text{B.}$ $(-3,-2) \cup(-2,+\infty)$
$\text{C.}$ $(-3,+\infty)$
$\text{D.}$ $(-\infty,-2) \cup(-2,+\infty)$
如图所示, U是全集,A,B是U的子集,则阴影部分所表示的集合是
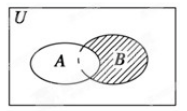
$\text{A.}$ $A \cap B$
$\text{B.}$ $A \cup B$
$\text{C.}$ $ B \cap(C_uA)$
$\text{D.}$ $A \cap\left ( C_uB\right)$
如果集合 $A=\left\{x | a x^2+2 x+1=0\right\}$ 中只有一个元素,则$a$的值为
$\text{A.}$ 0
$\text{B.}$ 0 或 1
$\text{C.}$ 1
$\text{D.}$ 不能确定
若集合 $S=\{y | y=3 x+2, x \in R\} ,T=\left\{y | y=x^2-1, x \in R\right\}$ 则 $S \cap T$ 是
$\text{A.}$ $S$
$\text{B.}$ $T$
$\text{C.}$ $\phi$
$\text{D.}$ 有限集
已知集合 $B=\{-1,1,4\}$ 满足条件 $ \phi \subsetneq M \subseteq B$ 的集合 $M$ 的个数为( $)$
$\text{A.}$ 3
$\text{B.}$ 6
$\text{C.}$ 7
$\text{D.}$ 8
已知函数 $f(3 x+1)=x^2+3 x+2$, 则 $f(4)=$
$\text{A.}$ 30
$\text{B.}$ 6
$\text{C.}$ 210
$\text{D.}$ 9
已知函数$f(x)=x^2+b x+c$,且$f(1)=0, f(3)=0$,则 $f(-1)=$
$\text{A.}$ 0
$\text{B.}$ 8
$\text{C.}$ 7
$\text{D.}$ 不确定
设 $A, B$ 是非空集合, 定义 $A \times B=(x | x \in A \cup B$, 且 $x \notin A \cap B]$, 已知 $A=\{x | 0 \leq x \leq 2], B=\{x | x \geq 0\}$, 则 $A \times B$ 等于=
$\text{A.}$ $(2,+\infty)$
$\text{B.}$ $[0,1] \cup i$
$\text{C.}$ $ [0,1] \cup [2,+\infty)$
$\text{D.}$ $[0,1] \cup(2,+\infty)$
已知集合 $A=\{x | 5 x-a \leq 0\}, B=\{x | 6 x-b>0\}, a, b \in N$, 且 $A \cap B \cap N=\{2,3,4\}$, 则整数对 $(a, b)$ 的个数为
$\text{A.}$ 20
$\text{B.}$ 25
$\text{C.}$ 30
$\text{D.}$ 42
填空题 (共 4 题 ),请把答案直接填写在答题纸上
方程组 $ \left\{\begin{array}{l}
x+2 y=4 \\
2 x-y=3
\end{array}\right. $ 的解集为
已知集合 $A=\{x | x>2\}, B=\{x | p x+5 < 0\}$, 且 $B \subseteq A$, 则 $p$ 的取值范围是
已知集合 $P=\left\{x | x^2=1\right\}$, 集合 $Q=\{x | a x=1]$, 若 $Q \subseteq P $, 那么 $a=$.
若函数 $f(x+3)$ 的定义域为 $[-5,-2]$, 则 $F(x)=f(x+1)+f(x-1)$ 的定义域为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设全集 $I=\left\{2,3, x^2+2 x-3\right], A=[5], C_I A=[2, y]$, 求 $x$, $y$ 的值.
已知集合 $A=\{x | 1 \leq x < 7\}, B=\{x | 2 < x < 10\}$, 全集为实数集R,
(1) 求 $A \cup B$;
(2) 求 $\left(C_{\mathbb{R}} A\right) \cap B $.
设集合 $A=\{x | 1-a \leq x \leq 1+a\}$, 集合 $B=\{x | x < -1$ 或 $x>5\}$, 分别就下列条件求实 数 $a$ 的取值范围:
(1) $A \cap B=\phi$;
(2) $A \cup B=B$.
(1) 已知二次函数 $f(x)$ 满足条件 $f(0)=1$ 及 $f(x+1)-f(x)=2 x$, 求 $f(x)$.
(2) 若 $f(x)$ 满足关系式 $f(x)+2 f\left(\frac{1}{x}\right)=3 x$, 求 $f(x)$.
已知集合 $A=\left\{x | x^2-3 x+2=0\right\} , B=\left\{x | x^2-a x+3 a-5=0\right\} $. 若 $A \cap B= B$, 求实数 $a$ 的取值范围.