单选题 (共 9 题 ),每题只有一个选项正确
当 $x \rightarrow 0$ 时, $\alpha(x), \beta(x)$ 是非零无穷小量,给出以下四个命题:
(1) 若 $\alpha(x) \sim \beta(x)$, 则 $\alpha^2(x) \sim \beta^2(x)$ ;
(2) 若 $\alpha^2(x) \sim \beta^2(x)$, 则 $\alpha(x) \sim \beta(x)$
(3) 若 $\alpha(x) \sim \beta(x)$ ,则 $\alpha(x)-\beta(x) \sim o(\alpha(x))$ ;
(4) 若 $\alpha(x)-\beta(x) \sim o(\alpha(x))$, 则 $\alpha(x) \sim \beta(x)$.
其中所有真命题序号是
$\text{A.}$ (1)(2)
$\text{B.}$ (1)(4)
$\text{C.}$ (1)(3)(4)
$\text{D.}$ (2)(3)(4)
设函数 $f(t)$ 连续,
$$
F(x, y)=\int_0^{x-y}(x-y-t) f(t) \mathrm{d} t
$$
则 $($ )
$\text{A.}$ $\frac{\partial F}{\partial x}=\frac{\partial F}{\partial y}, \frac{\partial^2 F}{\partial x^2}=\frac{\partial^2 F}{\partial y^2}$
$\text{B.}$ $\frac{\partial F}{\partial x}=\frac{\partial F}{\partial y}, \frac{\partial^2 F}{\partial x^2}=-\frac{\partial^2 F}{\partial y^2}$
$\text{C.}$ $\frac{\partial \boldsymbol{F}}{\partial x}=-\frac{\partial \boldsymbol{F}}{\partial y}, \frac{\partial^2 \boldsymbol{F}}{\partial x^2}=\frac{\partial^2 F}{\partial y^2}$
$\text{D.}$ $\frac{\partial F}{\partial x}=-\frac{\partial F}{\partial y}, \frac{\partial^2 F}{\partial x^2}=-\frac{\partial^2 F}{\partial y^2}$
已知 $I_1=\int_0^1 \frac{x}{2(1+\cos x)} \mathrm{d} x, I_2=\int_0^1 \frac{\ln (1+x)}{1+\cos x} \mathrm{~d} x$, $I_3=\int_0^1 \frac{2 x}{1+\sin x} \mathrm{~d} x$ ,则 $(\quad)$
$\text{A.}$ $I_1 < I_2 < I_3$
$\text{B.}$ $I_2 < I_1 < I_3$
$\text{C.}$ $I_1 < I_3 < I_2$
$\text{D.}$ $I_3 < I_2 < I_1$
设 $A$ 为三阶矩阵, $A=\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0\end{array}\right)$ ,则 $A$ 的特征值为 $1,-1,0$ 的充分必要条件是 ()
$\text{A.}$ 存在可逆矩阵 $\boldsymbol{P}, \boldsymbol{Q}$ ,使得 $\boldsymbol{A}=\boldsymbol{P} \boldsymbol{\Lambda} \boldsymbol{Q}$
$\text{B.}$ 存在可逆矩阵 $\boldsymbol{P}$ ,使得 $\boldsymbol{A}=\boldsymbol{P} \boldsymbol{\Lambda} \boldsymbol{P}^{-1}$
$\text{C.}$ 存在正交矩阵 $Q$ ,使得 $\boldsymbol{A}=\boldsymbol{Q} \boldsymbol{\Lambda} Q^{-1}$
$\text{D.}$ 存在可逆矩阵 $\boldsymbol{P}$ ,使得 $\boldsymbol{A}=\boldsymbol{P} \boldsymbol{\Lambda} \boldsymbol{P}^T$
设矩阵 $A=\left(\begin{array}{lll}1 & 1 & 1 \\ 1 & a & a^2 \\ 1 & b & b^2\end{array}\right), b=\left(\begin{array}{l}1 \\ 2 \\ 4\end{array}\right)$, 则 $A x=b$ 的解的情况为 ( )
$\text{A.}$ 无解
$\text{B.}$ 有解
$\text{C.}$ 有无穷多解或无解
$\text{D.}$ 有唯一解或无解
设 $\alpha_1=\left(\begin{array}{l}\lambda \\ 1 \\ 1\end{array}\right), \alpha_2=\left(\begin{array}{l}1 \\ \lambda \\ 1\end{array}\right), \alpha_3=\left(\begin{array}{l}1 \\ 1 \\ \lambda\end{array}\right), \alpha_4=\left(\begin{array}{c}1 \\ \lambda \\ \lambda^2\end{array}\right)$ ,若向量组 $\alpha_1, \alpha_2, \alpha_3$ 与 $\alpha_1, \alpha_2, \alpha_4$ 等价,则 $\lambda$ 的取值范围是( )
$\text{A.}$ $\{0,1\}$
$\text{B.}$ $\{\lambda \mid \lambda \in R, \lambda \neq-2\}$
$\text{C.}$ $\{\lambda \mid \lambda \in R$ 且 $\lambda \neq-1, \lambda \neq-2\}$
$\text{D.}$ $\{\lambda \mid \lambda \in R$ 且 $\lambda \neq-1\}$
设随机变量 $X \sim N(0,4)$, 随机变量 $Y \sim B\left(3, \frac{1}{3}\right)$, 且 $X$ 与 $Y$ 不相关,则 $D(X-3 Y+1)=( )$
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 10
设随机变量序列 $X_1, X_2, \cdots, X_n$ 独立同分布,且 $X_1$ 的概率密度为 $f(x)=\left\{\begin{array}{ll}1-|x|, \mid & x \mid < 1 \\ 0, & \text { 其他 }\end{array}, n \rightarrow \infty\right.$ 时, $\frac{1}{n} \sum_{i=1}^n X_i^2$依概率收敛于()
$\text{A.}$ $\frac{1}{8}$
$\text{B.}$ $\frac{1}{6}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
设二维随机变量 $(X, Y)$ 的概率分布
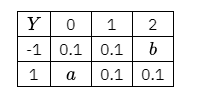
若事件 $\max \{(X, Y)=2\}$ 与事件 $\{\min (X, Y)=1\}$ 相互独立,则 $\operatorname{Cov}(X, Y)=($
$\text{A.}$ -0.6
$\text{B.}$ -0.36
$\text{C.}$ 0
$\text{D.}$ 0.48
填空题 (共 6 题 ),请把答案直接填写在答题纸上
极限 $\lim _{x \rightarrow 0}\left(\frac{1+e^x}{2}\right)^{\cot x}=$
$\int_0^2 \frac{2 x-4}{x^2+2 x+4} \mathrm{~d} x=$
已知函数 $f(x)=e^{\sin x}+e^{-\sin x}$ ,则 $f^{\prime \prime \prime}(2 \pi)=$
已知函数 $f(x)=\left\{\begin{array}{l}e^x, 0 \leq x \leq 1 \\ 0, \text { 其他 }\end{array}\right.$ ,则
$\int_{-\infty}^{+\infty} \mathrm{d} x \int_{-\infty}^{+\infty} f(x) f(y-x) \mathrm{d} y=$
设 $\boldsymbol{A}$ 为 3 阶矩阵,交换 $\boldsymbol{A}$ 的第二行和第三行, 再将第二列的 -1 倍加到第一列,得到矩阵 $\left(\begin{array}{ccc}-2 & 1 & -1 \\ 1 & -1 & 0 \\ -1 & 0 & 0\end{array}\right)$ ,则 $A^{-1}$的迹 $\operatorname{tr}\left(A^{-1}\right)=$
设 $A, B, C$ 为三个随机事件, $A$ 与 $B$ 互不相容, $A$ 与 $C$互不相容, $B$ 与 $C$ 相互独立,且
$$
P(A)=P(B)=P(C)=\frac{1}{3}
$$
则 $P(B \cup C \mid A \cup B \cup C)=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $y=y(x)$ 满足
$$
y^{\prime}+\frac{1}{2 \sqrt{x}} y=2+\sqrt{x}, y(1)=3
$$
求曲线 $y=y(x)$ 的渐近线.
设某产品的产量 $Q$ 由资本投入量 $\boldsymbol{x}$ 和劳动投入量 $y$ 决定,生产函数为 $Q=12 x^{\frac{1}{2}} y^6$ 。该产品的销售单价 $P$与 $Q$ 的关系为 $P=1160-1.5 Q$ ,若单位资本投入和单位劳动投入的价格分别为 6 和 8 ,求利润最大时的产量.
计算二重积分 $\iint_D \frac{(x-y)^2}{x^2+y^2} \mathrm{~d} x \mathrm{~d} y$ ,其中区域 $D$ 为 $y=x+2$ 与
$y=\sqrt{4-x^2}$ 以及 $x$ 轴所围成的区域。
求幂级数 $\sum_{n=0}^{\infty} \frac{(-4)^n+1}{4^n(2 n+1)} x^{2 n}$ 的收敛域及和函数 $S(x)$.
已知二次型
$$
f\left(x_1, x_2, x_3\right)=3 x_1^2+4 x_2^2+3 x_3^2+2 x_1 x_3 .
$$
(1) 求正交变换 $X=Q Y$ 将 $f\left(x_1, x_2, x_3\right)$ 化为标准形;
(2) 证明: $\min _{x \neq 0} \frac{f(x)}{x^T x}=2$.
设 $X_1, X_2, \cdots, X_n$ 为来自均值为 $\theta$ 的指数分布的简单随机样本, $Y_1, Y_2, \cdots, Y_m^{\ominus}$ 为来自均值为 $2 \theta$ 的指数分布总体的简单随机样本,且两样本相互独立,其中 $\theta(\theta>0)$为末知参数. 利用样本 $X_1, X_2, \cdots, X_n, Y_1, Y_2, \cdots, Y_m$ ,求 $\theta$的最大似然估计计量 $\hat{\theta}$ ,并求 $D(\hat{\theta})$.