单选题 (共 8 题 ),每题只有一个选项正确
函数 $f(x)=e^{x}-e x, x \in R$ 的单调递增区间是
$\text{A.}$ $(0,+\infty)$
$\text{B.}$ $(-\infty, 0)$
$\text{C.}$ $(-\infty, 1)$
$\text{D.}$ $(1,+\infty)$
已知 $f(x)$ 为偶函数,当 $x < 0$ 时,$f(x)=x^{3}-x$ ,则曲线 $y=f(x)$ 在点 $(1,0)$ 处的切线方程是
$\text{A.}$ $2 x-y-2=0$
$\text{B.}$ $4 x-y-4=0$
$\text{C.}$ $2 x+y-2=0$
$\text{D.}$ $4 x+y-4=0$
已知函数 $f(x)=x^{3}+a x^{2}-x$ 的图象在点 $A(1, f(1))$ 处的切线方程为 $y=4 x-3$ ,则函数 $y$ $=f(x)$ 的极大值为
$\text{A.}$ 1
$\text{B.}$ $-\frac{5}{27}$
$\text{C.}$ $-\frac{25}{27}$
$\text{D.}$ -1
如图,某公园需要修建一段围绕绿地的弯曲绿道(图中虚线)与两条直道(图中实线)平滑连续(相切),已知环绕绿地的弯曲绿道为某三次函数图象的一部分,则该函数的解析式为( )
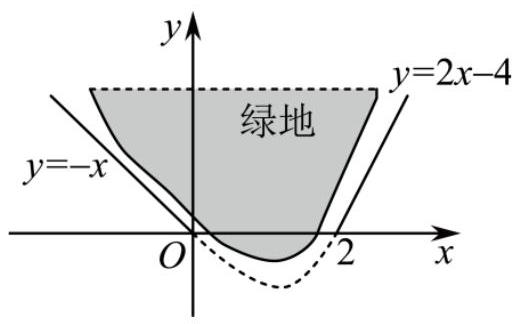
$\text{A.}$ $y=\frac{1}{4} x^{3}-x$
$\text{B.}$ $y=\frac{1}{4} x^{3}-x^{2}-x$
$\text{C.}$ $y=-\frac{1}{4} x^{3}+x$
$\text{D.}$ $y=-\frac{1}{4} x^{3}+x^{2}+x$
已知函数 $f(x)$ 的导函数的图象如右图所示,则下列结论正确的是
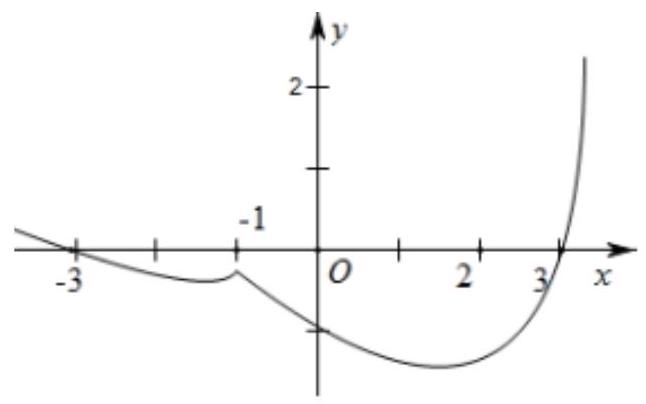
$\text{A.}$ -3 是 $f(x)$ 的极小值点
$\text{B.}$ -1 是 $f(x)$ 的极小值点
$\text{C.}$ $f(x)$ 在区间 $(-\infty, 3)$ 上单调递减
$\text{D.}$ 曲线 $y=f(x)$ 在 $x=2$ 处的切线斜率小于零
若函数 $f(x)=\left(2 x^{2}-m x+4\right) e^{x}$ 在区间 $[2,3]$ 上不是单调函数,则实数 $m$ 的取值范围是
$\text{A.}$ $\left[\frac{20}{3}, \frac{17}{2}\right]$
$\text{B.}$ $\left(\frac{20}{3}, \frac{17}{2}\right)$
$\text{C.}$ $\left[5, \frac{20}{3}\right]$
$\text{D.}$ $\left(5, \frac{20}{3}\right)$
已知函数 $f(x)=k x^{2}, g(x)=\ln x$ ,若存在 $x_{i} \in\left[\frac{1}{\mathrm{e}}, \mathrm{e}\right),(i=1,2)$ ,使得 $f\left(x_{i}\right)=g\left(x_{i}\right)$ , $(i=1,2)$ ,则实数 $k$ 的取值范围是( )
$\text{A.}$ $\left[\frac{1}{\mathrm{e}^{2}}, \frac{1}{2 \mathrm{e}}\right)$
$\text{B.}$ $\left(\frac{1}{2 e}, \frac{1}{e}\right)$
$\text{C.}$ $\left[\frac{1}{2 \mathrm{e}}, \frac{1}{\mathrm{e}}\right)$
$\text{D.}$ $\left(\frac{1}{\mathrm{e}^{2}}, \frac{1}{2 \mathrm{e}}\right)$
已知 $a=\frac{1}{\ln \sqrt{2}}, b=2 \sqrt{\mathrm{e}}, c=\frac{3 \sqrt[3]{\mathrm{e}^{4}}}{4}$(其中 e 为自然常数),则 $a 、 b 、 c$ 的大小关系为 ( )
$\text{A.}$ $a < c < b$
$\text{B.}$ $b < a < c$
$\text{C.}$ $c < b < a$
$\text{D.}$ $c < a < b$
多选题 (共 4 题 ),每题有多个选项正确
若直线 $y=\frac{1}{2} x+b(b \in R)$ 是曲线 $y=f(x)$ 的切线,则曲线 $y=f(x)$ 的方程可以是
$\text{A.}$ $f(x)=x^{3}+2 x^{2}+8$
$\text{B.}$ $f(x)=\tan x$
$\text{C.}$ $f(x)=e^{\frac{x}{2}}$
$\text{D.}$ $f(x)=\ln \frac{1}{2 x+1}$
已知 $f(x)=\frac{\ln x}{x}$ ,下列说法正确的是( )
$\text{A.}$ $f(x)$ 在 $x=1$ 处的切线方程为 $y=x-1$
$\text{B.}$ 单调递增区间为 $(-\infty, e)$
$\text{C.}$ $f(x)$ 的极大值为 $\frac{1}{e}$
$\text{D.}$ 方程 $f(x)=-1$ 有两个不同的解
已知函数 $y=f(x)$ 的导函数 $y=f^{\prime}(x)$ ,且 $f^{\prime}(x)=-\left(x-x_{1}\right)\left(x-x_{2}\right), x_{1} < x_{2}$ ,则
$\text{A.}$ $x_{2}$ 是函数 $y=f(x)$ 的一个极大值点
$\text{B.}$ $f\left(x_{1}\right) < f\left(x_{2}\right)$
$\text{C.}$ 函数 $y=f(x)$ 在 $x=\frac{x_{1}+2 x_{2}}{3}$ 处切线的斜率小于零
$\text{D.}$ $f\left(\frac{x_{1}+x_{2}}{2}\right)>0$
定义在 $(0,+\infty)$ 上的函数 $f(x)$ 满足 $2 f(x)+x f^{\prime}(x)=\frac{1}{x^{2}}, f(1)=0$ ,则下列说法正确的是( )
$\text{A.}$ $f(x)$ 在 $x=\sqrt{\mathrm{e}}$ 处取得极大值,极大值为 $\frac{1}{2 \mathrm{e}}$
$\text{B.}$ $f(x)$ 有两个零点
$\text{C.}$ 若 $f(x) < k-\frac{1}{x^{2}}$ 在 $(0,+\infty)$ 上恒成立,则 $k>\frac{\mathrm{e}}{2}$
$\text{D.}$ $f(1) < f(\sqrt{2}) < f(\sqrt{3})$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若直线 $y=-2 x+\frac{2}{3}$ 与曲线 $y=\frac{1}{3} x^{3}-a x$ 相切,则 $a=$ $\qquad$ .
函数 $f(x)=x^{2}-4 \mathrm{e}^{x}+1$ 的图象在点 $(0, f(0))$ 处的切线方程为 $\qquad$ .
已知函数 $f(x)$ 的定义域为 $(0,+\infty)$ ,其导函数为 $f^{\prime}(x)$ ,若 $x f^{\prime}(x)-1 < 0 . f(\mathrm{e})=2$ ,则关于 $x$ 的不等式 $f\left(\mathrm{e}^{x}\right) < x+1$ 的解集为 $\qquad$。
若函数 $f(x)=\mathrm{e}^{x}-a x^{2}-a$ 存在两个极值点 $x_{1}, x_{2}$ ,且 $x_{2}=2 x_{1}$ ,则 $a=$ $\qquad$ .
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\mathrm{e}^{x} \cos x-x$ .
(1)求曲线 $y=f(x)$ 在点 $(0, f(0))$ 处的切线方程;
(2)求函数 $f(x)$ 在区间 $\left[0, \frac{\pi}{2}\right]$ 上的最大值和最小值.
已知函数 $f(x)=\frac{1}{2} m x^{2}-2 a x+\ln x(m, a \in R)$ 在 $x=1$ 处的切线斜率为 $2-2 a$ .确定 $m$ 的值,并讨论函数 $f(x)$ 的单调性;
已知函数 $f(x)=x^{2}+x \ln x$ .
(1)求函数 $f(x)$ 在区间 $[1, \mathrm{e}]$ 上的最大值;
(2)若关于 $x$ 的方程 $f(x)=a x^{3}$ 有两个不相等的实数根,求实数 $a$ 的取值范围.
已知函数 $f(x)=\frac{\mathrm{e}^{x}-1}{\mathrm{e}^{x}+1}$(e为自然对数的底数).
(1)若不等式 $f(x) > \frac{\mathrm{e}-1}{\mathrm{e}+1}$ 恒成立,求实数 $x$ 的取值范围;
(2)若不等式 $f(x) < a x+\frac{1}{3}-a \ln 2$ 在 $x \in(\ln 2,+\infty)$ 上恒成立,求实数 $a$ 的取值范围.
已知函数 $f(x)=(x-2) \mathrm{e}^{x}$ .
(1)若 $a \in(0,+\infty)$ ,讨论 $f(x)$ 在 $(0, a)$ 上的单调性;
(2)若函数 $g(x)=f(x)-m(x-1)^{2}$ 在 $[1,2]$ 上的最大值小于 $-\frac{2 \mathrm{e}}{3}$ ,求 $m$ 的取值范围.
已知函数 $f(x)=x \mathrm{e}^{a x}-\mathrm{e}^{x}$ .
(1)当 $a=1$ 时,讨论 $f(x)$ 的单调性;
(2)当 $x > 0$ 时,$f(x) < -1$ ,求 $a$ 的取值范围;
(3)设 $n \in \mathbf{N}^{*}$ ,证明:$\frac{1}{\sqrt{1^{2}+1}}+\frac{1}{\sqrt{2^{2}+2}}+\mathrm{L}+\frac{1}{\sqrt{n^{2}+n}} > \ln (n+1)$ .