单选题 (共 8 题 ),每题只有一个选项正确
若 $(2-2 \mathrm{i}) z=\mathrm{i}$, 则 $\bar{z}=$
$\text{A.}$ $\frac{1}{4}+\frac{1}{4}{ }_1$
$\text{B.}$ $-\frac{1}{4}-\frac{1}{4} \mathrm{i}$
$\text{C.}$ $\frac{1}{4}-\frac{1}{4} \mathrm{i}$
$\text{D.}$ $-\frac{1}{4}+\frac{1}{4} \mathrm{i}$
从 1984 年第 23 届洛杉矶夏季奥运会到 2024 年第 33 届巴黎夏季奥运会,我国获得的夏季奥运会金牌数依次为 $1 \boldsymbol{\lambda}$ ई $16,16,28,644,51,38,26,38,40$ ,这 11 个数据的 $60 \%$ 分位数是
$\text{A.}$ 16
$\text{B.}$ 30
$\text{C.}$ 32
$\text{D.}$ 51
已知集合 $A=\left\{n \left\lvert\, \frac{n}{3} \in \mathbf{Z}\right.\right\}, B=\left\{n \left\lvert\, \frac{n}{4} \in \mathbf{Z}\right.\right\}, C=\left\{n \left\lvert\, \frac{n}{6} \in \mathbf{Z}\right.\right\}$, 则
$\text{A.}$ $A \cap B \varsubsetneqq C$
$\text{B.}$ $B \cup C=A$
$\text{C.}$ $C \varsubsetneqq A \cap B$
$\text{D.}$ $B \cap C \varsubsetneqq A \cap B$
$\left(\frac{2}{x^2}+\frac{3}{x^3}\right)(x-1)^7$ 的展开式中的常数项为
$\text{A.}$ 147
$\text{B.}$ -147
$\text{C.}$ 63
$\text{D.}$ -63
若函数 $f(x)=\log _{0.1}(12-a x)$ 在区间 $(3,6)$ 上单调递增, 则 $a$ 的取值范围是
$\text{A.}$ $(-\infty, 0)$
$\text{B.}$ $(-2,0)$
$\text{C.}$ $(0,2)$
$\text{D.}$ $(0,2]$
已知 $\tan \theta, \tan \left(\frac{8 \pi}{3}-\theta\right)$ 是一元二次方程 $x^2+a x-5=0$ 的两个根, 则 $a=$
$\text{A.}$ $6 \sqrt{3}$
$\text{B.}$ $-6 \sqrt{3}$
$\text{C.}$ $4 \sqrt{3}$
$\text{D.}$ $-4 \sqrt{3}$
在体积为 12 的三棱锥 $A-B C D$ 中, $A C \perp A D, B C \perp B D$, 平面 $A C D \perp$ 平面 $B C D, \angle A C D=\frac{\pi}{3}, \angle B C D=$ $\frac{\pi}{4}$, 若点 $A, B, C, D$ 都在球 $O$ 的表面上, 则球 $O$ 的表面积为
$\text{A.}$ $12 \pi$
$\text{B.}$ $16 \pi$
$\text{C.}$ $32 \pi$
$\text{D.}$ $48 \pi$
若函数 $f(x)=\left(x^2-2 \sqrt{2} x+\frac{1}{4} m\right) \sin \left(\frac{1}{4} m x-\frac{\pi}{3}\right)\left(m \in \mathbf{N}^*\right)$ 在[0,4] 上恰有3 个零点, 则符合条件的 $m$ 的个数是
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
多选题 (共 3 题 ),每题有多个选项正确
已知向量 $\boldsymbol{a}=(-2,1), \boldsymbol{b}=(t,-1)$, 则
$\text{A.}$ 若 $a \perp b$, 则 $t=-\frac{1}{2}$
$\text{B.}$ 若 $\boldsymbol{a}, \boldsymbol{b}$ 共线,则 $t=-2$
$\text{C.}$ $\boldsymbol{b}$ 不可能是单位向量
$\text{D.}$ 若 $t=0$, 则 $|2 \boldsymbol{a}-\boldsymbol{b}|=5$
我们把平面内到两个定点距离之积为常数的点的轨迹称为卡西尼卵形线. 在平面直角坐标系中,设定点为 $F_1(-1,0), F_2(1,0)$ ,动点 $P(x, y)$ 满足 $\left|P F_1\right|\left|P F_2\right|=4$ ,化简可得卡西尼卵形线 $C: x^2+y^2+1=2 \sqrt{ } x^2+4$, 则
$\text{A.}$ 曲线 $C$ 既是中心对称图形也是轴对称图形
$\text{B.}$ 曲线 $C$ 关于直线 $y=x$ 对称
$\text{C.}$ 曲线 $C$ 都在圆 $x^2+y^2=6$ 内
$\text{D.}$ 曲线 $C$ 与椭圆 $\frac{x^2}{3}+\frac{y^2}{2}=1$ 没有公共点
已知函数 $f(x)=\mathrm{e}^x, g(x)=\ln x$, 若 $f(x), g(x)$ 的图象与直线 $l_1: y=a_1 x+b_1$ 分别切于点 $A\left(x_1, y_1\right)$, $B\left(x_2, y_2\right)\left(x_1>x_2\right)$, 与直线 $l_2: y=a_2 x+b_2$ 分别切于点 $C, D$, 且 $l_1, l_2$ 相交于点 $P\left(x_0, y_0\right)$, 则
$\text{A.}$ $x_1-\ln x_2=0$
$\text{B.}$ $\mathrm{e}^{x_1}=\frac{x_1+1}{x_1-1}$
$\text{C.}$ $a_1>2-a_2$
$\text{D.}$ $x_0+y_0>\frac{2 \mathrm{e}^2}{\mathrm{e}^{x_1}-1}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知点 $P\left(1, y_0\right)$ 是抛物线 $C: y^2=2 p x(p>0)$ 上一点, 且点 $P$ 到 $C$ 的焦点距离为 2 , 则 $p=$
已知变量 $y$ 与 $x$ 线性相关, 由样本点 $\left(x_i, y_i\right)\left(x_i=i, i=1,2,3,4,5\right)$ 求得的回归方程为 $\hat{y}=\frac{1}{5} x+\hat{a}$,若点 $\left(x_5, y_5\right)$ 在回归直线上, 且 $y_5=2$, 则 $\sum_{=1} y_4=$
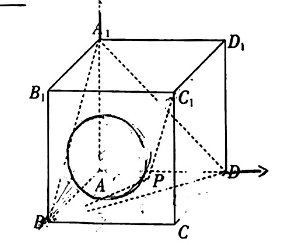
如图, 在棱长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $P$ 在 $\triangle A_1 B D$ 的边界及其内部运动, 且 $A P=$ $\sqrt{2}$, 则 $B P+C_1 P$ 的最大值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别为 $a, b, c$, 且 $a(1-3 \cos C)=3 c \cos A$.
(1) 求 $\frac{b}{a}$ 的值;
(2) 若 $c=2$, 求 $B$ 最大时 $\triangle A B C$ 的面积.
已知函数 $f(x)=\left(a+x-x^2\right) \mathrm{e}^x$.
(1) 若 $f(x)$ 在 $\mathbf{R}$ 上单调递减,求 $a$ 的取值范围;
(2) 若 $a=1$, 判断 $f(x)$ 是否有最大值, 若有, 求出最大值; 若没有, 请说明理由.
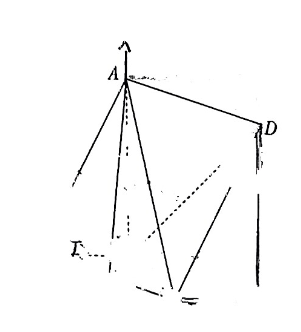
如图, 在四棱锥 $P-A B C D$ 中, 四边形 $A B C D$ 是平行四边形, $P A \perp P B, P B \perp P C \perp A=2 \sqrt{2}$, $P B=P C=\sqrt{2}, A B=A C$, 点 $E$ 在 $B C$ 上, 且 $A E=3$.
(1) 证明: $A D \perp$ 平面 $A P E$;
(2) 求直线 $A E$ 与平面 $P C D$ 所成角的正弦值.
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的一条渐近线的倾斜角为 $\frac{\pi}{3}, C$ 的右焦点 $F$ 到该渐近线的距离为 $2 \sqrt{3}$.
(1)求 $C$ 的方程;
(2) 若过 $F$ 的直线与 $C$ 的左、右支分别交于点 $A, B$, 与圆 $O: x^2+y^2=a^2$ 交于与 $A, B$ 不重合的 $M$, $N$ 两点。
(i) 求直线 $A B$ 斜率的取值范围;
(ii) 求 $|A B| \cdot|M N|$ 的取值范围.
记数列 $\left\{a_n\right\}$ 中前 $k$ 项的最大值为 $b_k$, 数列 $\left\{b_n\right\}$ 称为 $\left\{a_n\right\}$ 的 " $M$ 数列",由所有 $b_n$ 的值组成的集合为 $C$ 。
(1) 若 $a_n=(n+a)\left(\frac{8}{9}\right)^n$, 且 $C$ 中有 3 个元素,求 $a$ 的取值范围;
(2) 若数列 $\left\{a_n\right\},\left\{b_n\right\}$ 都只有 4 项, $\left\{b_n\right\}$ 为 $\left\{a_n\right\}$ 的" $M$ 数列",满足 $a_k \in\{2,4,6,8\}(k=1,2,3,4)$且存在 $i \in\{1,2,3,4\}$, 使得 $b_i=8$, 求符合条件的数列 $\left\{b_n\right\}$ 的个数;
(3)若 $a_n=n \sin \frac{n \pi}{2} ,\left\{a_n\right\}$ 的" $M$ 数列" $\left\{b_n\right\}$ 的前 $n$ 项和为 $S_n$ ,从 $S_1, S_2, S_3, \cdots, S_{4 n}(n \geqslant 3)$ 中任取 3 个,记其中能被 2 整除且不能被 4 整除的个数为 $X$ ,求 $E X$ 。