一、单选题 (共 15 题 ),每题只有一个选项正确
1. 方程 的解是
2. 把复数 对应的向量按顺时针方向旋转 所得到的向量对应的复数是
3. 如果底面直径和高相等的圆柱的侧面积是 S , 那么圆柱的体积等于
4. 方程 在区间 内的解的个数是
1
2
3
4
5. 已知如图是函数
的图象, 那么
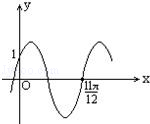
6. 函数 的值域是
7. 如果直线 与直线 关于直线 对称,那么
8. 极坐标方程 表示的曲线是
圆
椭圆
双曲线的一支
抛物线
9. 设全集 , 集合 . 那么 等于
10. 若实数 、 满足 , 则 的最大值为
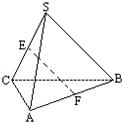
11. 如图, 正三棱锥
的侧棱与底面边长相等, 如果
、 分别为
、 的中点, 那么异面直线 EF 与 SA 所成的角等于
12. 已知 . 设命题甲为: 两个实数 满足 ; 命题乙为: 两个实数 满足 且 . 那么
甲是乙的充分条件, 但不是乙的必要条件
甲是乙的必要条件, 但不是乙的充分条件
甲是乙的充分条件
甲不是乙的充分条件, 也不是乙的必要条件
13. A, B, C, D, E 五人并排站成一排, 如果 B 必须站在 A 的右边 (A, B 可以不相邻), 那么不同的排法共有
24 种
60 种
90 种
120 种
14. 以一个正方体的顶点为顶点的四面体共有
70 个
64 个
58 个
52 个
15. 设函数 的图象沿 x 轴正方向平移 2 个单位所得到的图象为 C . 又设图象 与 关于原点对称, 那么 所对应的函数是
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
16. 双曲线 的准线方程是
17. 的展开式中, 的系数等于
18. 已知 是公差不为零的等差数列, 如果 是 的前 项的和, 那么 等于
19. 函数 的最大值是
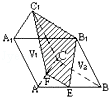
20. 如图, 三棱柱
中, 若
、 分别为
、 的中点, 平面
将三棱柱分成体积为
、 的两部分, 那么
三、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
21. 有四个数, 其中前三个数成等差数列, 后三个数成等比数列, 并且第一个数与第四个数的和是 16 , 第二个数与第三个数的和是 12 , 求这四个数.
22. 已知 , 求 的值.
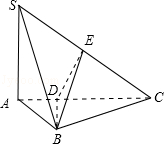
23. 如图, 在三棱锥
中,
底面
垂直平分
, 且分别交
、 于
、
E. 又
. 求以
为棱, 以
与
为面的二面角的度数.
24. 设 a 为实数, 在复数集 C 中解方程: .
25. 设椭圆的中心是坐标原点, 长轴在 x 轴上, 离心率 , 已知点 到这个椭圆上的点最远距离是 . 求这个椭圆的方程, 并求椭圆上到点 P 的距离等于 的点的坐标.
26. , 其中 是实数, 是任意自然数且 .
(I) 如果 当 时有意义, 求 的取值范围;
(II) 如果 , 证明 当 时成立.