单选题 (共 9 题 ),每题只有一个选项正确
已知 $\lim _{\Delta x \rightarrow 0} \frac{f(3+\Delta x)-f(3-\Delta x)}{\Delta x}=2$, 则 $f^{\prime}(3)=$
$\text{A.}$ -1
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 4
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 已知 $a_2+2 a_4+a_{10}=68$, 则 $S_9=$
$\text{A.}$ 272
$\text{B.}$ 270
$\text{C.}$ 157
$\text{D.}$ 153
若随机变量 $X \sim N\left(90, \sigma^2\right)$ 且 $P(X \leq 70)=0.12$, 则 $P(90 \leq X \leq 110)=$
$\text{A.}$ 0.12
$\text{B.}$ 0.24
$\text{C.}$ 0.28
$\text{D.}$ 0.38
已知 $P(A)=\frac{1}{5}, P(B \mid A)=\frac{1}{2}, P(\bar{B} \mid \bar{A})=\frac{5}{8}$, 则 $P(B)=$
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{1}{6}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{3}{8}$
已知由样本数据 $\left(x_i, y_i\right)(i=1,2,3, \cdots, 10)$ 组成的一个样本, 变量 $x, y$ 具有线性相关关系, 其经验回归方程为 $y=\hat{b} x+\hat{a}$, 并计算出变量 $x, y$ 之间的相关系数为 $-0.96, \sum_{i=1}^{10} x_i=-8$, $\sum_{i=1}^{10} y_i=-15$, 则经验回归直线经过
$\text{A.}$ 第一、二、三象限
$\text{B.}$ 第二、三、四象限
$\text{C.}$ 第一、二、四象限
$\text{D.}$ 第一、三、四象限
根据分类变量 $X$ 与 $Y$ 的抽样数据, 计算得到 $\chi^2=3.452$ 依据 $\alpha=0.1$ 的独立性检验 $\left(x_{0.1}=2.706\right)$ 则下面说法正确的是
$\text{A.}$ 变量 $X$ 与 $Y$ 不独立, 该推断犯错误的概率不超过 0.1
$\text{B.}$ 变量 $X$ 与 $Y$ 不独立, 该推断犯错误的概率不低于 0.1
$\text{C.}$ 变量 $X$ 与 $Y$ 独立, 该推断犯错误的概率不超过 0.1
$\text{D.}$ 变量 $X$ 与 $Y$ 独立, 该推断犯错误的概率不低于 0.1
甲、乙、丙、丁四个城市准备竞争新能源汽车、半导体、通信设备、风电设备、石油冶炼这五个项目, 每个城市至少能竞得一个项目. 每个项目有且只有一个城市竞得, 则丁城市既没有竞得风电设备项目, 又没有竞得石油冶炼项目的概率为
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{21}{40}$
$\text{D.}$ $\frac{7}{8}$
设随机变量 $X \sim H(10, M, 1000)$ ( $2 \leq M \leq 992$ 且 $\left.M \in \mathbf{N}^*\right)$, $H(2 ; 10, M, 1000)$ 最大时, $E(X)=$
$\text{A.}$ 1.98
$\text{B.}$ 1.99
$\text{C.}$ 2.00
$\text{D.}$ 2.01
已知 $a>0, b>0, c>0$, 且 $a, b, c$ 成等差数列, 随机变量 $X$ 的分布列为
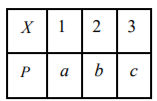
下列选项正确的是
$\text{A.}$ $b=\frac{1}{4}$
$\text{B.}$ $a+c=\frac{2}{3}$
$\text{C.}$ $\frac{4}{3} < E(X) < \frac{8}{3}$
$\text{D.}$ $D(X)$ 的最大值为 $\frac{2}{3}$
多选题 (共 2 题 ),每题有多个选项正确
已知 $f(x)=(2 x-3)^n\left(n \in \mathbf{N}^*\right)$ 展开式的二项式系数和为 512 , $f(x)=a_0+a_1(x-1)+a_2(x-1)^2+\ldots+a_n(x-1)^n$, 下列选项正确的是
$\text{A.}$ $a_1+a_2+\ldots+a_n=1$
$\text{B.}$ $a_1+2 a_2+3 a_3+\ldots+n a_n=18$
$\text{C.}$ $a_2=144$
$\text{D.}$ $\left|a_0\right|+\left|a_1\right|+\ldots+\left|a_n\right|=3^9$
已知函数 $f(x)$ 与其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathrm{R}$, 且 $f(x)-x$ 与 $f^{\prime}(1-2 x)$均为偶函数, 则
$\text{A.}$ $f(x+1)$ 为偶函数
$\text{B.}$ $\frac{f(x)}{x}-1(x \neq 0)$ 为奇函数
$\text{C.}$ $f^{\prime}(x+2)+f^{\prime}(x)=2$
$\text{D.}$ $f^{\prime}(0)=0$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
$\left(2 x^2+1\right)\left(x-\frac{1}{x}\right)^6$ 的展开式中的常数项为 $\qquad$ . (请用数字作答)
$\mathrm{e}^{2 x}+\frac{1}{x+1}-\frac{1}{2} x$ 在 $x=0$ 处的切线的倾斜角为 $\alpha$, 则 $\cos 2 \alpha=$
产品抽样检查中经常遇到一类实际问题, 假定在 $N$ 件产品中有 $M$件不合格品, 在产品中随机抽 $n$ 件做检查, 发现 $k$ 件不合格品的概率为 $P(X=k)=\frac{\mathrm{C}_M^k \mathrm{C}_{N-M}^{n-k}}{\mathrm{C}_N^n}, k=t, t+1, \cdots, s$, 其中 $s$ 是 $M$ 与 $n$ 中的较小者, $t$ 在 $n$ 不大于合格品数(即 $n \leq N-M$ )时取 0 , 否则 $t$ 取 $n$ 与合格品数之差, 即 $t=n-(N-M)$. 根据以上定义及分布列性质, 请计算当 $N=16, M=8$ 时, $\mathrm{C}_8^0 \mathrm{C}_8^4+\mathrm{C}_8^1 \mathrm{C}_8^3+\mathrm{C}_8^2 \mathrm{C}_8^2+\mathrm{C}_8^3 \mathrm{C}_8^1+\mathrm{C}_8^4 \mathrm{C}_8^0=$ $\qquad$ :若 $N=2 n, M=n$, 请计算 $\mathrm{C}_n^0 \mathrm{C}_n^1+\mathrm{C}_n^1 \mathrm{C}_n^2+\mathrm{C}_n^2 \mathrm{C}_n^3+\cdots+\mathrm{C}_n^{n-2} \mathrm{C}_n^{n-1}+\mathrm{C}_n^{n-1} \mathrm{C}_n^n=$ $\qquad$ . (两空均用组合数表示)
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, S_n=\frac{5}{2} n^2-\frac{1}{2} n\left(n \in \mathbf{N}^*\right)$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=\frac{1}{a_n a_{n+1}}$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
已知函数 $f(x)=x^2 \mathrm{e}^x$.
(1) 求函数 $f(x)$ 的单调区间.
(2) 若对 $\forall x \in[-1,2], f(x)-m>0$ 恒成立, 求实数 $m$ 的取值范围.
中国国际大数据产业博览会(简称“数博会”)从 2015 年在贵阳开办, 至今已过 9 年.某校机器人社团为了解贵阳市市民对历年“数博会”科技成果的关注情况, 在贵阳市随机抽取了 1000 名市民进行问卷调查, 问卷调查的成绩 $\xi$ 近似服从正态分布 $N\left(77, \sigma^2\right)$, 且
$P(77 \leq \xi \leq 80)=0.3 \text {. }$
(1) 估计抽取市民中问卷成绩在 80 分以上的市民人数;
(2) 若本次问卷调查得分超过 80 分, 则认为该市民对“数博会”的关注度较高, 现从贵阳市随机抽取 3 名市民, 记对“数博会”关注度较高的市民人数为随机变量 $X$, 求 $X$ 的分布列和数学期望.
近年来, 共享单车进驻城市, 绿色出行引领时尚. 某公司计划对未开通共享单车的 $A$ 县城进行车辆投放, 为了确定车辆投放量, 对过去在其他县城的投放量情况以及年使用人次进行了统计, 得到了投放量 $x$ (单位; 千辆) 与年使用人次 $y$ (单位: 千次) 的数据如下表所示, 根据数据绘制投放量 $x$ 与年使用人次 $y$ 的散点图如图所示.
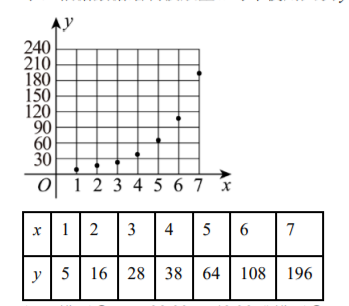
拟用模型(1) $y=28.32 x-48.28$ 或模型(2) $y=10^{c+d x}$ 对两个变量的关系进行拟合, 令 $t=\lg y$, 可得 $\sum_{i=1}^7 y_1=455, \sum_{i=1}^7 t_i=11.06, \sum_{i=1}^7 x_i^2=140, \sum_{i=1}^7 x_i y_i=2613, \sum_{i=1}^7 x_i t_i=51.04$, 变量 $y$ 与 $t$ 的标准差分别为 $s_y=62.23, s_t=0.494$.
(1)根据所给的统计量, 求模型(2) 中 $y$ 关于 $x$ 的回归方程;(结果保留小数点后两位)
(2) 计算并比较两种模型的相关系数 $r$ (结果保留小数点后三位), 求哪种模型预测值精度更高、更可靠;
(3)已知每辆单车的购入成本为 200 元,年调度费以及维修等的使用成本为每人次 0.2 元, 按用户每使用一次, 收费 1 元计算, 若投入 8000 辆单车, 利用 (2) 中更可靠的模型, 预测几年后开始实现盈利. (结果保留整数)
附, 样本点 $\left(x_i, y_i\right)(i=1,2, \cdots, n)$ 的线性回归方程 $\hat{y}=\hat{a}+\hat{b} x$ 最小二乘估计公式为 $\hat{b}=\frac{\sum_{i=1}^n x_i y_i-n \overline{x y}}{\sum_{i=1}^n x_i^2-n \bar{x}^2}$, $\hat{a}=\bar{y}-\hat{b} \bar{x}$, 相关系数 $r=\frac{\sum_{i=1}^n x_i y_i-n \overline{x y}}{\sqrt{\sum_{i=1}^n x_i^2-n \bar{x}^2} \cdot \sqrt{\sum_{i=1}^n y_i^2-n \bar{y}^2}}$参考数据: $10^{2.54} \approx 347$.
已知集合 $\mathrm{A}$ 中含有三个元素 $x, y, z$, 同时满足 ① $x < y < z$; ② $x+y>z$; ③ $x+y+z$ 为偶数, 那么称集合 $\mathrm{A}$ 具有性质 $P$. 已知集合 $S_n=\{1,2,3, \cdots, 2 n\}\left(n \in \mathrm{N}^*, n \geq 4\right)$, 对于集合 $S_n$ 的非空子集 $B$, 若 $S_n$ 中存在三个互不相同的元素 $a, b, c$, 使得 $\boldsymbol{a}+\boldsymbol{b}, \boldsymbol{b}+\boldsymbol{c}, \boldsymbol{c}+\boldsymbol{a}$ 均属于 $B$, 则称集合 $B$是集合 $S_n$ 的“期待子集”.
(1) 试判断集合 $A=\{1,2,3,5,7,9\}$ 是否具有性质 $P$, 并说明理由;
(2) 若集合 $B=\{3,4, a\}$ 具有性质 $P$, 证明: 集合 $B$ 是集合 $S_4$ 的“期待子集”;
(3) 证明:集合 $M$ 具有性质 $P$ 的充要条件是集合 $M$ 是集合 $S_n$ 的“期待子集”.