数学试题讲解

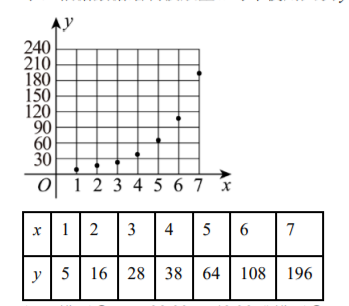
近年来, 共享单车进驻城市, 绿色出行引领时尚. 某公司计划对未开通共享单车的

A

县城进行车辆投放, 为了确定车辆投放量, 对过去在其他县城的投放量情况以及年使用人次进行了统计, 得到了投放量

x

(单位; 千辆) 与年使用人次

y

(单位: 千次) 的数据如下表所示, 根据数据绘制投放量

x

与年使用人次

y

的散点图如图所示.

拟用模型(1)

y = 28.32 x - 48.28

或模型(2)

y = 10^{c + d x}

对两个变量的关系进行拟合, 令

t = \lg y

, 可得

\sum_{i = 1}^{7} y_{1} = 455, \sum_{i = 1}^{7} t_{i} = 11.06, \sum_{i = 1}^{7} x_{i}^{2} = 140, \sum_{i = 1}^{7} x_{i} y_{i} = 2613, \sum_{i = 1}^{7} x_{i} t_{i} = 51.04

, 变量

y

与

t

的标准差分别为

s_{y} = 62.23, s_{t} = 0.494

.
（1）根据所给的统计量, 求模型(2) 中

y

关于

x

的回归方程;（结果保留小数点后两位）
(2) 计算并比较两种模型的相关系数

r

(结果保留小数点后三位), 求哪种模型预测值精度更高、更可靠;
（3）已知每辆单车的购入成本为 200 元，年调度费以及维修等的使用成本为每人次 0.2 元, 按用户每使用一次, 收费 1 元计算, 若投入 8000 辆单车, 利用 (2) 中更可靠的模型, 预测几年后开始实现盈利. (结果保留整数)

附, 样本点

(x_{i}, y_{i}) (i = 1, 2, \dots, n)

的线性回归方程

\hat{y} = \hat{a} + \hat{b} x

最小二乘估计公式为

\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \overset{―}{x y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}

\hat{a} = \bar{y} - \hat{b} \bar{x}

, 相关系数

r = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \overset{―}{x y}}{\sqrt{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} \cdot \sqrt{\sum_{i = 1}^{n} y_{i}^{2} - n {\bar{y}}^{2}}}

参考数据:

10^{2.54} \approx 347