单选题 (共 5 题 ),每题只有一个选项正确
设 $\vec{T}^{\circ}=(\cos \alpha, \cos \beta)$ 是简单封闭曲线 $L$ 上点 $(x, y)$ 处指向逆时钟方向的单位切向量,则该点处指向曲线外侧的单位法向量 $\vec{n}^{\circ}=$
$\text{A.}$ $(-\cos \alpha,-\cos \beta)$
$\text{B.}$ $(\cos \beta, \cos \alpha)$
$\text{C.}$ $(\cos \beta,-\cos \alpha)$
$\text{D.}$ $(-\cos \beta, \cos \alpha)$
向量场 $\vec{u}(x, y, z)=x y^2 \vec{i}+y e^z \vec{j}+x \vec{k}$ 在点 $P(1,1,0)$ 处的旋度为
$\text{A.}$ $(1,1,2)$
$\text{B.}$ $(-1,-1,-2)$
$\text{C.}$ $2$
$\text{D.}$ $-2$
已知方程 $\left(x^2+a x y+y^3\right) \mathrm{d} x+\left(x^2+b x y^2+2 y\right) \mathrm{d} y=0$为全微分方程,则常数 $a, b$ 的取值为
$\text{A.}$ $a=2, b=3$
$\text{B.}$ $a=3, b=2$
$\text{C.}$ $a=-2, b=3$
$\text{D.}$ $a=2, b=-3$
已知向量场 $\mathrm{F}(x, y)=(P(x, y), Q(x, y))$ ,如题图所示, $L$ 为圆周 $x^2+y^2=1$ ,且取逆时针方向,则曲线积分
$\oint_L P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y>0$ 所对应的向量场是
$\text{A.}$ 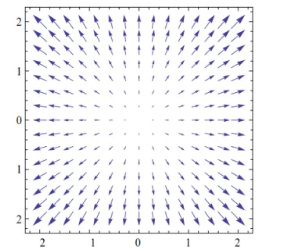 $\text{B.}$
$\text{B.}$ 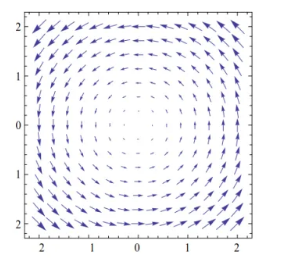 $\text{C.}$
$\text{C.}$ 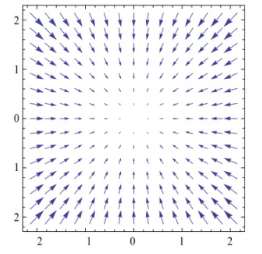 $\text{D.}$
$\text{D.}$ 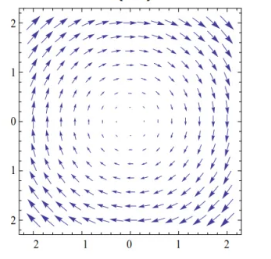
下列正向闭曲线中, 使曲线积分 $\oint_I \frac{y \mathrm{~d} x-x \mathrm{~d} y}{x^2+x y+y^2}=0$ 的曲线是
$\text{A.}$ $L: x^2+y^2=1$
$\text{B.}$ $L: x^2+x y+y^2=1$
$\text{C.}$ $L:(x-1)^2+(y-1)^2=1$
$\text{D.}$ $L: x^{\frac{2}{3}}+y^{\frac{2}{3}}=1$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
设 $L: y=\frac{x^2}{2}(0 \leq x \leq 1)$ ,则曲线积分 $\int_L x \mathrm{~d} s$ 值为
设曲线 $C: x^2+y^2-2 x+4 y+1=0$ ,则曲线积分 $\int_C(x+y) \mathrm{d} s=$
在力场 $\vec{F}=(-y, x)$ 的作用下,质点在以 $(0,0),(1,0),(0,1)$ 为顶点的三角形上沿顺时针方向运动一周,则在该过程中力场对质点所做的功是
曲线积分 $\oint_L\left(x-\frac{y}{x^2+y^2}\right) \mathrm{d} x+\left(y+\frac{x}{x^2+y^2}\right) \mathrm{d} y=$ $\qquad$其中 $L: \frac{x^2}{9}+\frac{y^2}{4}=1$ 为逆时针方向.
已知曲面 $\Sigma: x^2+y^2+z^2=a^2(a>0)$ ,则 $\oint_{\Sigma}(x+z)^2 \mathrm{~d} S$的值为
解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $f(u, v)=\oint_C\left(u x^2+v y^2\right) \mathrm{d} s$ ,其中曲线 $C: x^2$ $+y^2=u^2$ ,试求 $f_{u v}^{\prime \prime}(1,1)$ 的值.
问: 当常数 $a$ 为何值时, 存在可微函数 $u=u(x, y)$, 使得 $\mathrm{d} u=(x-2 y+1) \mathrm{d} x+\left(a x+y^2+3\right) \mathrm{d} y$ ? 若 $u(0,0)=0$,求函数 $u(x, y)$ 的表达式.
设 $f(x)$ 为正值连续函数,证明不等式:
$$
I=\oint_C x f(y) \mathrm{d} y-\frac{y}{f(x)} \mathrm{d} x \geq 2 \pi a^2,
$$
其中 $C$ 是 $(x-a)^2+(y-a)^2=a^2(a>0)$ ,方向取逆时钟方向.
设三元函数 $f(x, y, z)$ 连续, $f(x, y, z) \neq 0$ 且满足 $f(x, y, z) \iiint_{\Omega} f(x, y, z) \mathrm{d} V=\left(x^2+y^2+z^2\right) \oint_{\Sigma} f(x, y, z) \mathrm{d} S$,其中 $\Omega$ 为球面 $\Sigma: x^2+y^2+z^2=1$ 所围成的闭区域,求 $f(x, y, z)$ 的表达式.
已知 $C$ 为不经过原点的简单光滑闭曲线,且取逆时针方向. 计算曲线积分 $\oint_C \frac{y \mathrm{~d} x-x \mathrm{~d} y}{a x^2+b y^2}$ ,其中 $a, b$ 为大于零的常数.
设函数 $f(t)$ 在 $(-\infty,+\infty)$ 上有连续导数, $L$ 为从点 $A\left(-\frac{\pi}{2},-1\right)$ 沿曲线 $y=\sin x$ 到点 $B\left(\frac{\pi}{2}, 1\right)$ ,再沿直线 $y=1$ 到点 $C\left(-\frac{\pi}{2}, 1\right)$ 的有向曲线段,计算曲线积分
$$
\int_L x f\left(x^2+y^2\right) \mathrm{d} x+x^2 \mathrm{~d} y .
$$
设有一边长为 1 的立方体,其一个顶点位于坐标原点,三条棱与坐标轴正方向重合,平面 $x+2 y+3 z=4$ 截立方体所得截面的边界线记作 $\Gamma$ ,计算
$$
I=\oint_{\Gamma}(x-y) \mathrm{d} x+(y-2 z) \mathrm{d} y+(z-3 x) \mathrm{d} z ,
$$
其中 $\Gamma$ 方向为从 $z$ 轴正向往负向看为逆时针方向.
设 $S$ 为旋转抛物面 $z=4-x^2-y^2 , \pi$ 为其在 $M(1,1,2)$ 处的切平面.
(1) 求 $S$ 在 $z \geq 0$ 部分的曲面面积.
(2) 求第一卦限介于 $S$ 与 $\pi$ 之间部分的体积.
设函数 $f(x)$ 具有二阶连续导数,且 $f(0)=1, f^{\prime}(0)=1$.假设对任意光滑闭曲面 $\boldsymbol{\Sigma}$ ,恒有
$$
\oint_{\Sigma}\left[f^{\prime}(x)+x^2\right] \mathrm{d} y \mathrm{~d} z+(z+1) f(x) \mathrm{d} x \mathrm{~d} y=0 .
$$
试求 $f(x)$ 的表达式.
计算曲面积分
$$
I=\iint_{\Sigma} x(8 y+1) \mathrm{d} y \mathrm{~d} z+2\left(1-y^2\right) \mathrm{d} z \mathrm{~d} x-4 y z \mathrm{~d} x \mathrm{~d} y \text {, }
$$
曲面,它的法向量与 $y$ 轴正向的夹角恒大于 $\frac{\pi}{2}$.
设二元函数 $f(x, y)$ 连续, 且满足
$f(x, y)=x^2 \oint_L f(x, y) \mathrm{d} s+x y \iint_D f(x, y) \mathrm{d} \sigma-1 \text { , }
$
其中 $D$ 为圆周 $L: x^2+y^2=1$ 所围成的闭区域.
(1) 试求 $f(x, y)$ 的表达式;
(2) 试证明: $\oint_L y f(x, y) \mathrm{d} x+x f(x, y) \mathrm{d} y=\frac{\pi}{2} \oint_L f(x, y) \mathrm{d} s$ ,
其中 $L$ 为逆时针方向.