单选题 (共 8 题 ),每题只有一个选项正确
拋物线 $y^2=2 p x$ 过点 $(2,2)$, 则焦点坐标为
$\text{A.}$ $(0,0)$
$\text{B.}$ $\left(\frac{1}{4}, 0\right)$
$\text{C.}$ $\left(\frac{1}{2}, 0\right)$
$\text{D.}$ $(1,0)$
已知平面向量 $\vec{a}=(3,2), \vec{b}=(-2,1)$, 若 $(\vec{a}+\lambda \vec{b}) \perp \vec{b}$, 则 $\lambda=$
$\text{A.}$ $-\frac{4}{5}$
$\text{B.}$ $-\frac{3}{5}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{4}{5}$
已知角 $\alpha\left(0^{\circ} < \alpha < 360^{\circ}\right)$ 终边上 $A$ 点坐标为 $\left(\sin 310^{\circ}, \cos 310^{\circ}\right)$, 则 $\alpha=$
$\text{A.}$ $130^{\circ}$
$\text{B.}$ $140^{\circ}$
$\text{C.}$ $220^{\circ}$
$\text{D.}$ $230^{\circ}$
设等比数列 $\left\{a_n\right\}$ 的首项为 1 , 公比为 $q$, 前 $n$ 项和为 $S_n$, 若 $\left\{S_n+1\right\}$ 也是等比数列, 则 $q=$
$\text{A.}$ -2
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
过点 $P(-2,0)$ 作圆 $C: x^2+y^2-4 x-4=0$ 的两条切线, 切点分别为 $A, B$, 则四边形 $P A C B$ 的面积为
$\text{A.}$ 4
$\text{B.}$ $4 \sqrt{2}$
$\text{C.}$ 8
$\text{D.}$ $8 \sqrt{2}$
设 $x>0$, 函数 $y=x^2+x-7, y=2^x+x-7, y=\log _2 x+x-7$ 的零点分别为 $a, b, c$, 则
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < a < c$
$\text{C.}$ $a < c < b$
$\text{D.}$ $c < a < b$
设 $x_1, x_2$ 是函数 $f(x)=x^3+a x^2+x+1$ 的两个极值点, 若 $x_1+3 x_2=-2$, 则 $a=$
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
已知 $f(x)=a \mathrm{e}^{x-1}-\ln x+\ln a, g(x)=(1-\mathrm{e}) x$, 当 $x>0$ 时, $\mathrm{e} f(x) \geq g(x)$, 则 $a$ 的取值范围为
$\text{A.}$ $\left(\frac{1}{e}, 1\right)$
$\text{B.}$ $\left(\frac{1}{e},+\infty\right)$
$\text{C.}$ $(1,+\infty)$
$\text{D.}$ $(e,+\infty)$
多选题 (共 3 题 ),每题有多个选项正确
已知函数 $f(x)=\sqrt{3} \sin x+\cos x$, 则
$\text{A.}$ $y=f(x)$ 的最大值为 2
$\text{B.}$ $y=f(x)$ 的图象关于点 $\left(\frac{\pi}{3}, 0\right)$ 对称
$\text{C.}$ $y=f(x)$ 在 $\left(0, \frac{\pi}{6}\right)$ 上单调递增
$\text{D.}$ 直线 $x=\frac{\pi}{6}$ 是 $y=f(x)$ 图象的一条对称轴
在 $\triangle A B C$ 中, $\angle A C B=\frac{\pi}{2}, A C=B C=2 \sqrt{2}, D$ 是 $A B$ 的中点. 将 $\triangle A C D$ 沿着 $C D$ 翻折, 得到三棱椎 $A^{\prime}-B C D$,则
$\text{A.}$ $C D \perp A^{\prime} B$.
$\text{B.}$ 当 $A^{\prime} D \perp B D$ 时, 三棱椎 $A^{\prime}-B C D$ 的体积为 4 .
$\text{C.}$ 当 $A^{\prime} B=2 \sqrt{3}$ 时, 二面角 $A^{\prime}-C D-B$ 的大小为 $\frac{2 \pi}{3}$.
$\text{D.}$ 当 $\angle A^{\prime} D B=\frac{2 \pi}{3}$ 时, 三棱椎 $A^{\prime}-B C D$ 的外接球的表面积为 $20 \pi$.
已知点 $A(-1,0), B(1,0)$, 直线 $A M, B M$ 相交于点 $M$, 且它们的斜率之和是 2. 设动点 $M(x, y)$ 的轨迹为曲线 $C$,则
$\text{A.}$ 曲线 $C$ 关于原点对称
$\text{B.}$ $x$ 的范围是 $\{x \mid x \neq 0\}, y$ 的范围是 $\mathbf{R}$
$\text{C.}$ 曲线 $C$ 与直线 $y=x$ 无限接近,但永不相交
$\text{D.}$ 曲线 $C$ 上两动点 $P(a, b), Q(c, d)$, 其中 $a < 0, c>0$, 则 $|P Q|_{\text {min }}=2 \sqrt{2 \sqrt{2}-2}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
已知双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的渐近线方程为 $y= \pm \frac{3}{4} x$, 则其离心率为
记 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 已知 $a_n=\left\{\begin{array}{c}\frac{1}{n(n+2)}, n \text { 为奇数, } \\ a_{n-1}, n \text { 为偶数, }\end{array}\right.$ 则 $S_{10}=$
已知 $A_1, A_2, A_3, A_4, A_5$ 五个点, 满足: $\overrightarrow{A_n A_{n+1}} \cdot \overrightarrow{A_{n+1} A_{n+2}}=0(n=1,2,3)$, $\left|A_n A_{n+1}\right|\left|A_{n+1} A_{n+2}\right|=n(n=1,2,3)$, 则 $\left|\overrightarrow{A_1 A_5}\right|$ 的最小值为
已知 $f(x)=(2 x+1) \ln x-\frac{x^2}{2}$, 曲线 $f(x)$ 在 $x=1$ 处的切线方程为 $y=a x+b$.
(1) 求 $a, b$;
(2) 证明 $f(x) \leq a x+b$.
① $S_3=7 a_3$, ②$a_2=\frac{1}{4}$, ③ $a_4, a_3, 6 a_5$ 成等差, 这三个条件中任选两个, 补充到下面问题中, 并解答本题.
设正项等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 满足 $\qquad$
(1) 求 $a_n$;
(2) 求数列 $\left\{n a_n\right\}$ 的前 $n$ 项和 $T_n$.
在 $\triangle A B C$ 中, 点 $M, N$ 分别为 $B C, A C$ 的中点, $A M$ 与 $B N$ 交于点 $G, A M=3, \angle M A B=45^{\circ}$.
(1) 若 $A C=5 \sqrt{2}$, 求中线 $B N$ 的长;
(2) 若 $\triangle A B C$ 是锐角三角形, 求四边形 $G M C N$ 面积的取值范围.
某市为繁荣地方经济, 大力实行人才引进政策, 为了解政策的效果, 统计了 2018-2023 年人才引进的数量 $y$ (单位: 万人), 并根据统计数据绘制了如图所示的散点图 ( $x$ 表示年份代码, 年份代码 1-6 分别代表 20182023 年).
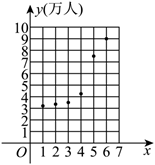
(1) 根据散点图判断 $y=b_{\ln } x+a$ 与 $y=e^{c+d x}$ ( $a, b, c, d$ 均为常数) 哪一个适合作为 $y$ 关于 $x$ 的回归方程类
型;(给出结论即可, 不必说明理由)
(2) 根据 (1) 的结果及表中的数据, 求出 $y$ 关于 $x$ 的回归方程, 并预测该市 2025 年引进人才的数量;
(3) 从这 6 年中随机抽取 4 年, 记引进人才数量超过 4 万人的年数为 $X$, 求 $X$ 的分布列和数学期望.
参考数据:
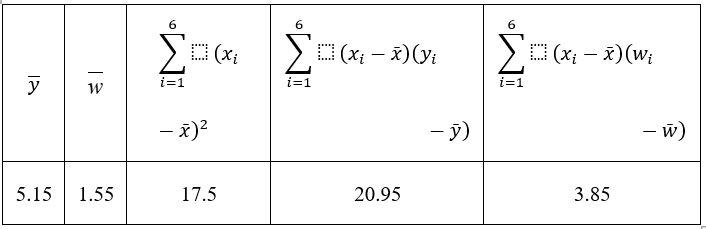
其中 $\bar{w}=\frac{1}{6} \sum_{i=1}^6 w_i, w_i=\ln y_i, \mathrm{e}^{2.44} \approx 11.47, \mathrm{e}^{2.54} \approx 12.68$.
参考公式: 对于一组数据 $\left(u_1, v_1\right),\left(u_2, v_2\right), \cdots,\left(u_n, v_n\right)$, 其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计分别为: $\hat{\beta}=\frac{\sum_{i=1}^n \prod\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n m\left(u_i-\bar{u}\right)^2}, \hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}$.
在平面直角坐标系 $x O y$ 中, 重新定义两点 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 之间的“距离”为 $|A B|=\left|x_2-x_1\right|+\mid y_2-$ $y_1 \mid$, 我们把到两定点 $F_1(-c, 0), F_2(c, 0)(c>0)$ 的“距离”之和为常数 $2 a(a>c)$ 的点的轨迹叫“椭圆”.
(1) 求“椭圆”的方程;
(2)根据“椭圆”的方程,研究“椭圆”的范围、对称性,并说明理由;
(3) 设 $c=1, a=2$, 作出“椭圆”的图形, 设此“椭圆”的外接椭圆为 $C, C$ 的左顶点为 $A$, 过 $F_2$ 作直线交 $C$ 于 $M, N$ 两点, $\triangle A M N$ 的外心为 $Q$, 求证: 直线 $O Q$ 与 $M N$ 的斜率之积为定值.