某市为繁荣地方经济, 大力实行人才引进政策, 为了解政策的效果, 统计了 2018-2023 年人才引进的数量 $y$ (单位: 万人), 并根据统计数据绘制了如图所示的散点图 ( $x$ 表示年份代码, 年份代码 1-6 分别代表 20182023 年).

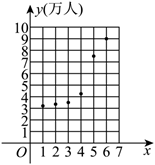
(1) 根据散点图判断 $y=b_{\ln } x+a$ 与 $y=e^{c+d x}$ ( $a, b, c, d$ 均为常数) 哪一个适合作为 $y$ 关于 $x$ 的回归方程类

型;（给出结论即可, 不必说明理由）
(2) 根据 (1) 的结果及表中的数据, 求出 $y$ 关于 $x$ 的回归方程, 并预测该市 2025 年引进人才的数量;
(3) 从这 6 年中随机抽取 4 年, 记引进人才数量超过 4 万人的年数为 $X$, 求 $X$ 的分布列和数学期望.

参考数据:

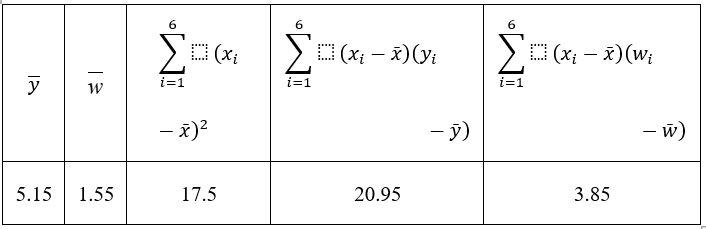
其中 $\bar{w}=\frac{1}{6} \sum_{i=1}^6 w_i, w_i=\ln y_i, \mathrm{e}^{2.44} \approx 11.47, \mathrm{e}^{2.54} \approx 12.68$.
参考公式: 对于一组数据 $\left(u_1, v_1\right),\left(u_2, v_2\right), \cdots,\left(u_n, v_n\right)$, 其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计分别为: $\hat{\beta}=\frac{\sum_{i=1}^n \prod\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n m\left(u_i-\bar{u}\right)^2}, \hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}$.