一、单选题 (共 12 题 ),每题只有一个选项正确
1. 在式子 中, 分式的个数为
2 个
3个
4个
5个
2. 下列运算正确的是
3. 若 、 是函数 的图象上的两点, 且 , 则 与 的大小关系为
无法判断
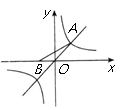
4. 如图, 已知点
是函数
与
的图象在第一象限内的交点, 点
在
轴负半轴上,且
, 则
的面积为
2
4
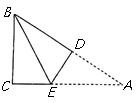
5. 如图, 在三角形纸片
中,
, 将
沿
折叠, 使点
与点
重合, 则折痕
的长为
1
2
6. 的三边长分别为 、、, 下列条件: (1) ; (2) : 5 ; (3) ; (4) , 其中能判断 是直角三角形的个数有
1个
2个
3个
4个
7. 一个四边形, 对于下列条件: (1)一组对边平行, 一组对角相等; (2)一组对边平行, 一条对角线被另一条对角线平分; (3)一组对边相等, 一条对角线被另一条对角线平分; (4)两组对角的平分线分别平行, 不能判定为平行四边形的是
(1)
(2)
(3)
(4)
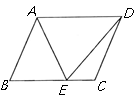
8. 如图, 已知
是菱形
的边
上一点, 且
, 那么
的度数为
9. 某班抽取 6 名同学进行体育达标测试, 成绩如下: . 下列关于对这组数据的描述错误的是
众数是 80
平均数是 80
中位数是 75
极差是 15
10. 某居民小区本月 1 日至 6 日每天的用水量如图所示, 那么这 6 天的平均用水量是
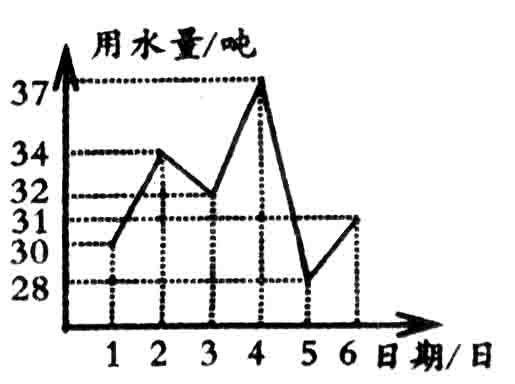
33 吨
32 吨
31 吨
30 吨
11. 如图, 直线
与双曲线
交于
、 两点,
轴于
, 连接
交
轴于
, 下列结论: (1)
、 关于原点对称; (2)
的面积为定值; (3)
是
的中点; (4)
. 其中正确结论的个数为

1 个
2 个
3 个
4 个
12. 如图, 在梯形 中, 交 于 是 的中点, , , 下列结论: (1) ; (2) ; (3) ; (4) , 其中正确的是
(1)(2)(3)
(2)(3)(4)
(1)(3)(4)
(1)(2)(3)(4)
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
13. 已知一组数据 的众数与它的平均数相等, 则这组数的中位数是
14. 观察式子: , 根据你发现的规律知, 第 8 个式子为
15. 已知梯形的中位线长 , 它被一条对角线分成两段, 这两段的差为 , 则梯形的两底长分别为
16. 直线 与双曲线 交于点 , 与 轴交于点 , 则
17. 已知直角坐标系中, 四边形 是矩形, 点 , 点 , 点 是 的中点, 点 是 边上的一个动点, 当 是等腰三角形时, 点 的坐标为
三、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
18. 解方程:
19. 先化简, 再求值: , 其中 .
20. 如图, 已知一次函数
的图象与反比例函数
的图象交于
,
两点, 连接
、.
(1) 求两个函数的解析式; (2) 求
的面积.
21. 小军八年级上学期的数学成绩如下表所示:


(1)计算小军上学期平时的平均成绩;
(2)如果学期总评成绩按扇形图所示的权重计算,问小军上学期的总评成绩是多少分?
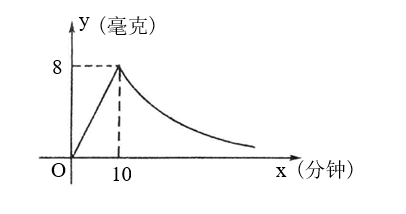
22. 为预防甲型 H1N1 流感, 某校对教室喷酒药物进行消毒. 已知喷酒药物时每立方米空气中的含药量
(毫克) 与时间
(分钟) 成正比, 药物喷酒完后,
与
成反比例 (如图所示). 现测得 10 分钟喷酒完后, 空气中每立方米的含药量为 8 毫克.
(1) 求喷酒药物时和喷酒完后,
关于
的函数关系式;
(2) 若空气中每立方米的含药量低于 2 毫克学生方可进教室, 问消毒开始后至少要经过多少分钟, 学生才能回到教室?
(3) 如果空气中每立方米的含药量不低于 4 毫克, 且持续时间不低于 10 分钟时, 才能杀灭流感病毒, 那么此次消毒是否有效? 为什么?
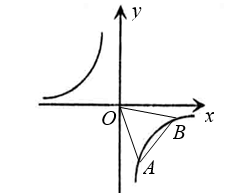
23. 如图, 直线
交坐标轴于
、 两点, 交双曲线
于点
, 过
作两坐标轴的垂线
、, 连接 OD.
(1) 求证:
平分
;
(2) 对任意的实数
, 求证
为定值;
(3) 是否存在直线
, 使得四边形
为平行四边形? 若存在, 求出直线的解析式;若不存在, 请说明理由.
