单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\{1,2,3\}, B=\{-1,0,1\}$, 则 $A \cup B=$
$\text{A.}$ $\{1\}$
$\text{B.}$ $\{0,1,2,3\}$
$\text{C.}$ $\{-1,0,1,2,3\}$
$\text{D.}$ $\{-1,0,2,3\}$
已知 $\mathrm{i}$ 为虚数单位, 则 $\frac{\mathrm{i}}{3-4 \mathrm{i}}=$
$\text{A.}$ $\frac{4+3 \mathrm{i}}{5}$
$\text{B.}$ $\frac{-4+3 i}{5}$
$\text{C.}$ $\frac{4+3 \mathrm{i}}{25}$
$\text{D.}$ $\frac{-4+3 \mathrm{i}}{25}$
已知向量 $a=(1, \lambda), b=(\mu,-2)$, 且 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 共线, 则
$\text{A.}$ $\frac{\lambda}{\mu}=-2$
$\text{B.}$ $\frac{\lambda}{\mu}=2$
$\text{C.}$ $\lambda \mu=-2$
$\text{D.}$ $\lambda \mu=2$
有一组样本数据 $1,3,2, a, 3,5,4, b$, 则
$\text{A.}$ 这组样本数据的极差不小于 4
$\text{B.}$ 这组样本数据的平均数不小于 4
$\text{C.}$ 这组样本数据的中位数不小于 3
$\text{D.}$ 这组样本数据的众数等于 3
条件 $p:|x|>|y|$, 条件 $q: \frac{1}{|x|} < \frac{1}{y}$, 则 $p$ 是 $q$ 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知抛物线 $C: y^2=2 p x(p>0), F$ 为抛物线 $C$ 的焦点, $P$ 为抛物线 $C$ 上的动点 (不含原点), $\odot F$ 的半径为 $\frac{p}{2}$, 若 $\odot P$ 与 $\odot F$ 外切, 则
$\text{A.}$ $\odot P$ 与直线 $x=0$ 相切
$\text{B.}$ $\odot P$ 与直线 $y=0$ 相切
$\text{C.}$ $\odot P$ 与直线 $x=-\frac{p}{2}$ 相切
$\text{D.}$ $\odot P$ 与直线 $y=-\frac{p}{2}$ 相切
已知 $a>0, b>0,2 a+b=a b$, 则 $\frac{2 a}{a-1}+\frac{b}{b-2}$ 的最小值为
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ $4 \sqrt{2}$
$\text{D.}$ $3+2 \sqrt{2}$
如图, 水利潍溉工具筒车的转轮中心 $O$ 到水面的距离为 $1 \mathrm{~m}$, 筒车的半径是 $3 \mathrm{~m}$, 盛水筒的初始位置为 $P_0, O P_0$ 与水平正方向的夹角为 $\frac{\pi}{6}$. 若简车以角速度 $2 \mathrm{rad} / \mathrm{min}$ 沿逆时针方向转动, $t$ 为筒车转动后盛水筒第一次到达入水点 $P_1$ 所需的时间(单位: $\mathrm{min}$ ), 则
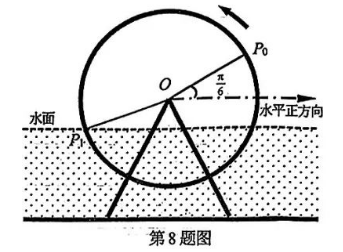
$\text{A.}$ $\cos t=\frac{1}{2}$
$\text{B.}$ $\sin t=\frac{\sqrt{2}}{2}$
$\text{C.}$ $\cos 2 t=-\frac{2 \sqrt{6}+1}{6}$
$\text{D.}$ $\sin 2 t=-\frac{\sqrt{3}+2 \sqrt{2}}{6}$
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $A C$ 与 $B D$ 交于点 $O$, 则
$\text{A.}$ $A C / /$ 平面 $B A_1 C_1$
$\text{B.}$ $D_1 O / /$ 平面 $B A_1 C_1$
$\text{C.}$ 平面 $A C D_1 / /$ 平面 $B A_1 C_1$
$\text{D.}$ 平面 $O D D_1 / /$ 平面 $B A_1 C_1$
已知函数 $f(x)=\frac{1}{3} x^3-4 x+4(x \in[0,3])$, 则
$\text{A.}$ 函数 $f(x)$ 在区间 $[0,2]$ 上单调递减
$\text{B.}$ 函数 $f(x)$ 在区间 $[0,3]$ 上的最大值为 1
$\text{C.}$ 函数 $f(x)$ 在点 $(1, f(1))$ 处的切线方程为 $y=-3 x+\frac{10}{3}$
$\text{D.}$ 若关于 $x$ 的方程 $f(x)=a$ 在区间 $[0,3]$ 上有两解,则 $a \in\left(-\frac{4}{3}, 4\right)$
对于给定的数列 $\left\{a_n\right\}$, 如果存在实数 $p, q$, 使得 $a_{n+1}=p a_n+q$ 对任意 $n \in \mathrm{N}^*$ 成立, 我们称数列 $\left\{a_n\right\}$是 “线性数列” , 数列 $\left\{c_n\right\}$ 满足 $c_1=1, c_{n+1}=c_n+b_n\left(n \in \mathrm{N}^*\right)$, 则
$\text{A.}$ 等差数列是 “线性数列”
$\text{B.}$ 等比数列是 “线性数列”
$\text{C.}$ 若 $\left\{b_n\right\}$ 是等差数列,则 $\left\{c_n\right\}$ 是 “线性数列”
$\text{D.}$ 若 $\left\{b_n\right\}$ 是等比数列,则 $\left\{c_n\right\}$ 是 “线性数列”
已知函数 $f(x)$ 和其导函数 $g(x)$ 的定义域都是 $\mathbf{R}$, 若 $f(x)-x$ 与 $g(2 x+1)$ 均为偶函数, 则
$\text{A.}$ $f(0)=0$
$\text{B.}$ $\frac{f(x)}{x}$ 关于点 $(0,1)$ 对称
$\text{C.}$ $g(2023)=1$
$\text{D.}$ $(g(1)-1) \times(g(2)+1)+(g(2)-1) \times(g(3)+1)+\cdots+(g(2023)-1) \times(g(2024)+1)=0$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
在二项式 $\left(x+\frac{1}{\sqrt{x}}\right)^5$ 的展开式中, $x^2$ 的系数为
已知梯形 $A B C D$ 满足 $A D / / B C$ 且 $A B \perp A D$, 其中 $B C=3, A B=\sqrt{3}, A D=2$, 将梯形 $A B C D$ 绕边 $B C$ 旋转一周, 所得到几何体的体积为
一次朕两枚骰子, 若两枚骰子点数之和为 4 或 5 或 6 , 则称这是一次成功试验. 现进行四次试验, 则恰出现一次成功试验的概率为
已知 $P$ 为椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上一点, $F_1, F_2$ 分别为其左右焦点, $A$ 为其右顶点, $O$为坐标原点, 点 $A$ 到直线 $O P$ 的距离为 $d_1\left(d_1 \neq 0\right)$, 点 $P$ 到 $x$ 轴的距离为 $d_2$, 若 $d_2=\frac{\sqrt{3}}{2} d_1$, 且 $\left|P F_1\right|,|P O|,\left|P F_2\right|$ 成等比数列, 则椭圆 $C$ 的离心率为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别是 $a, b, c$, 且 $\sin ^2 A+\sin ^2 B-\sin ^2 C=\sin A \sin B$.
(I)求角 $C$;
(II) $D$ 为边 $B C$ 上一点, 且 $C D=B D=2 A C$, 求 $\cos \angle D A B$ 的值.
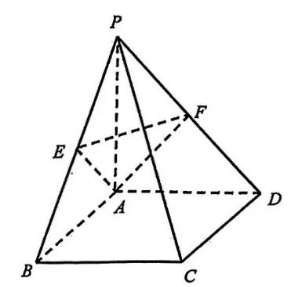
如图, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为正方形, 侧棱 $P A \perp$ 底面 $A B C D$, 且 $P A=A B$, 点 $E, F$ 分别为 $P B, P D$ 的中点.
(I)证明: $P C \perp$ 平面 $A E F$;
(II)求平面 $A E F$ 与平面 $A B C D$ 夹角的余弦值.
设正项数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_n=\frac{a_n^2+a_n}{2}$.
(I)求数列 $\left\{a_n\right\}$ 的通项公式;
(II)若不等式 $\frac{1}{3 S_1}+\frac{1}{4 S_2}+\cdots+\frac{1}{(n+2) S_n}>\frac{1}{2}-\frac{\lambda}{S_n}$ 对任意正整数 $n$ 均成立, 求 $\lambda$ 的取值范围.
2023 年 9 月 8 日, 第 19 届亚运会火炬传递启动仪式在杭州西湖景区涌金公园广场成功举行.火炬传递首日传递从杭州西湖涌金公园广场出发, 沿南山路一湖滨路—环城西路一北山街一西泠桥一孤山路传递, 在 “西湖十景” 之一的平湖秋月收火. 杭州亚运会火炬首日传递共有 106 棒火炬手参与.
(I)组委会从全省火炬手中随机抽取了 100 名火炬手进行信息分析, 得到如下表格:
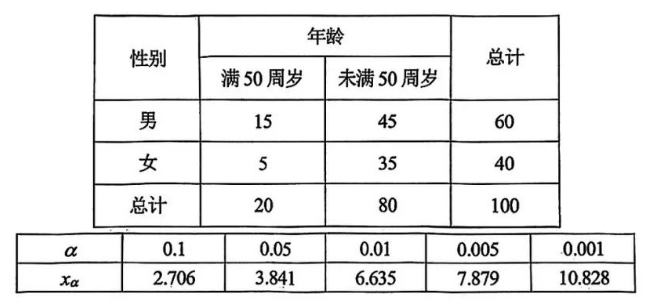
根据小概率值 $\alpha=0.1$ 的 $\chi^2$ 独立性检验, 试判断全省火炬手的性别与年龄满或未满 50 周岁是否有关联;
(II)在全省的火炬手中, 男性占比 $72 \%$, 女性占比 $28 \%$, 且 $50 \%$ 的男性火炬手和 $25 \%$ 的女性火炬手喜欢观看足球比赛. 某电视台随机选取一位喜欢足球比赛的火炬手做访谈, 请问这位火炬手是男性的概率为多少?
已知双曲线 $C: \frac{x^2}{2}-\frac{y^2}{2}=1$, 直线 $l$ 过双曲线 $C$ 的右焦点 $F$ 且交右支于 $A, B$ 两点, 点 $S$ 为线段 $A B$ 的中点, 点 $T$ 在 $x$ 轴上, $S T \perp A B$.
(I) 求双曲线 $C$ 的渐近线方程;
(II) 若 $\overrightarrow{T S} \cdot \overrightarrow{T B}=\frac{80}{9}$, 求直线 $l$ 的方程.
已知 $f(x)=a x^2-a x-\frac{1}{x}-\ln x+\mathrm{e}^{1-x}(a>0)$.
(I) 若当 $x=1$ 时函数 $f(x)$ 取到极值, 求 $a$ 的值;
(II)讨论函数 $f(x)$ 在区间 $(1,+\infty)$ 上的零点个数.