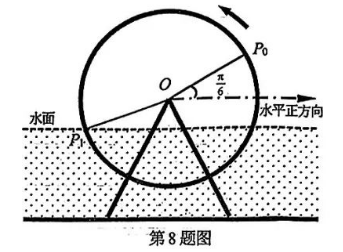
如图, 水利潍溉工具筒车的转轮中心 $O$ 到水面的距离为 $1 \mathrm{~m}$, 筒车的半径是 $3 \mathrm{~m}$, 盛水筒的初始位置为 $P_0, O P_0$ 与水平正方向的夹角为 $\frac{\pi}{6}$. 若简车以角速度 $2 \mathrm{rad} / \mathrm{min}$ 沿逆时针方向转动, $t$ 为筒车转动后盛水筒第一次到达入水点 $P_1$ 所需的时间(单位: $\mathrm{min}$ ), 则

A. $\cos t=\frac{1}{2}$
B. $\sin t=\frac{\sqrt{2}}{2}$
C. $\cos 2 t=-\frac{2 \sqrt{6}+1}{6}$
D. $\sin 2 t=-\frac{\sqrt{3}+2 \sqrt{2}}{6}$