单选题 （共 10 题 ），每题只有一个选项正确
设函数 $f(x)=\left\{\begin{array}{cc}g(x) \cos \frac{1}{x^2}, & x \neq 0, \\ 0, & x=0,\end{array}\right.$ 且 $g(0)=g^{\prime}(0)=0$, 则 $f(x)$ 在点 $x=0$ 处
$\text{A.}$ 连续但不可导.
$\text{B.}$ 可导但 $f^{\prime}(0) \neq 0$.
$\text{C.}$ 极限存在但不连续.
$\text{D.}$ 可微且 $\left.\mathrm{d} f(x)\right|_{x=0}=0$.
设在极坐标系下, 区域的表示为 $D=\{(r, \theta) \mid 0 \leqslant \theta \leqslant 2 \pi, r \leqslant 1\}$, 记
$$
\begin{aligned}
& I_1=\int_0^{2 \pi} \mathrm{d} \theta \int_0^1(\cos r+r \cos \theta+r \sin \theta) r \mathrm{~d} r, \\
& I_2=\int_0^{2 \pi} \mathrm{d} \theta \int_0^1\left(\cos r^2-r \cos \theta+r \sin \theta\right) r \mathrm{~d} r, \\
& I_3=\int_0^{2 \pi} \mathrm{d} \theta \int_0^1\left(\cos r^4-r \cos \theta-r \sin \theta\right) r \mathrm{~d} r,
\end{aligned}
$$
则
$\text{A.}$ $I_1 < I_2 < I_3$.
$\text{B.}$ $I_2 < I_1 < I_3$.
$\text{C.}$ $I_3 < I_2 < I_1$.
$\text{D.}$ $I_3 < I_1 < I_2$.
设函数 $y=y(x)$ 是微分方程 $y^{\prime \prime \prime}-y^{\prime \prime}-y^{\prime}+y=0$ 的解, 在 $x=0$ 处 $y(x)$ 取得极值 4 , 且 $y^{\prime \prime}(0)=$ 0 , 则 $y(x)=$
$\text{A.}$ $\left(3-2 x^2\right) \mathrm{e}^x+\mathrm{e}^{-x}$.
$\text{B.}$ $3 \mathrm{e}^x+x \mathrm{e}^{-x}$.
$\text{C.}$ $(3-2 x) \mathrm{e}^x+\mathrm{e}^{-x}$.
$\text{D.}$ $\mathrm{e}^x+(3-2 x) \mathrm{e}^{-x}$.
已知级数 $\sum_{n=1}^{\infty}(-1)^n\left(\mathrm{e}^{\frac{1}{\sqrt{n}}}-1\right) \ln \left(1+\frac{1}{n^\alpha}\right)$ 绝对收敛, 级数 $\sum_{n=1}^{\infty}(-1)^n \frac{1}{n^{1-\sigma}}$ 条件收敛, 则
$\text{A.}$ $\alpha>\frac{5}{2}$.
$\text{B.}$ $2 < \alpha < 3$.
$\text{C.}$ $\frac{1}{2} < \alpha < 1$.
$\text{D.}$ $\alpha < 3$.
已知 $\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}, \boldsymbol{D}$ 都是 4 阶非零矩阵, 且 $\boldsymbol{A B C D}=\boldsymbol{O}$, 如果 $|\boldsymbol{B C}| \neq 0$, 记 $r(\boldsymbol{A})+r(\boldsymbol{B})+r(\boldsymbol{C})+r(\boldsymbol{D})$ $=r$, 则 $r$ 的最大值是
$\text{A.}$ 11
$\text{B.}$ 12
$\text{C.}$ 13
$\text{D.}$ 14
三元一次方程组
$$
\left\{\begin{array}{l}
x_1+x_2+a x_3=4 \\
x_1-x_2+2 x_3=-4 \\
-x_1+a x_2+x_3=a^2
\end{array}\right.
$$
所代表的三平面不可能的位置关系为
$\text{A.}$ 
$\text{B.}$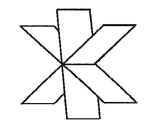 
$\text{C.}$ 
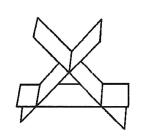$\text{D.}$ 
矩阵 $\boldsymbol{A}=\left[\begin{array}{cc}1 & -1 \\ -1 & 1\end{array}\right]$,与 $\boldsymbol{A}$ 合同但不相似的矩阵为
$\text{A.}$ $\left[\begin{array}{ll}1 & 1 \\ 1 & 1\end{array}\right]$.
$\text{B.}$ $\left[\begin{array}{ll}2 & 0 \\ 0 & 0\end{array}\right]$.
$\text{C.}$ $\left[\begin{array}{ll}3 & 0 \\ 0 & 0\end{array}\right]$.
$\text{D.}$ $\left[\begin{array}{ll}-1 & -1 \\ -1 & -1\end{array}\right]$.
已知随机变量 $X_1$ 与 $X_2$ 的分布函数分别为 $F_1(x)$ 与 $F_2(x)$. 我们假设: 如果 $X_i$ 为离散型随机变量, 其概率分布为 $X_i \sim\left(\begin{array}{cc}0 & 1 \\ 1-p_i & p_i\end{array}\right)$ (即 $X_i$ 服从参数为 $p_i$ 的 $0-1$ 分布, $0 < p_i < 1, i=1,2$ ).如果 $X_i$ 为连续型随机变量, 其概率密度为 $f_i(x)(i=1,2)$, 已知 $F_1(x) \leqslant F_2(x)$, 则
$\text{A.}$ $p_1 \leqslant p_2$.
$\text{B.}$ $p_1 \geqslant p_2$.
$\text{C.}$ $f_1(x) \leqslant f_2(x)$.
$\text{D.}$ $f_1(x) \geqslant f_2(x)$.
设 $X_1, X_2, \cdots, X_n$ 是来自总体 $N(0,1)$ 的简单随机样本, 记 $\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$, 则 $D\left(\bar{X}^2\right)=$
$\text{A.}$ $\frac{1}{n^2}$.
$\text{B.}$ $\frac{2}{n^2}$.
$\text{C.}$ $\frac{3}{n^2}$.
$\text{D.}$ $\frac{4}{n^2}$.
已知随机变量 $X$ 的概率密度为 $f(x)$, 则随机变量函数 $Y=|X|$ 的概率密度 $f_Y(y)$ 为
$\text{A.}$ $f_Y(y)=f(y)+f(-y)$.
$\text{B.}$ $f_Y(y)=\frac{f(y)+f(-y)}{2}$.
$\text{C.}$ $f_Y(y)=\left\{\begin{array}{cc}f(y)+f(-y), & y>0, \\ 0, & y \leqslant 0 .\end{array}\right.$
$\text{D.}$ $f_Y(y)=\left\{\begin{array}{cc}\frac{f(y)+f(-y)}{2}, & y>0, \\ 0, & y \leqslant 0 .\end{array}\right.$
填空题 （共 6 题 ），请把答案直接填写在答题纸上
设函数 $z=f(x, y)$ 的二阶偏导数存在, $\frac{\partial^2 z}{\partial y^2}=4$, 且 $f(x, 0)=2, f_y^{\prime}(x, 0)=x^2$, 则 $f(x, y)=$
积分 $I=\int_0^{\frac{\pi}{2}} \mathrm{~d} \theta \int_0^{2 \cos \theta}\left[(r \cos \theta-1)^3+r \sin \theta\right] r \mathrm{~d} r=$
设 $\Sigma$ 为圆柱面 $x^2+y^2=4(0 \leqslant z \leqslant 1)$, 则 $\iint_{\Sigma}\left(x^2+y\right) \mathrm{d} S=$
设函数 $z=f(x, y)$ 在点 $(0,2)$ 的某邻域内可微, 且 $f(x, y+2)=2+3 x+4 y+o(\rho)$, 其中 $\rho=$ $\sqrt{x^2+y^2}$, 则曲面 $z=f(x, y)$ 在点 $(0,2)$ 处的全微分为
设 $\boldsymbol{A}$ 为 2 阶矩阵, $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2$ 是矩阵 $\boldsymbol{A}$ 分别属于特征值 0,2 的特征向量, 则方程组 $\boldsymbol{A x}=\boldsymbol{\alpha}_2$ 的通解为
设 $X_1, X_2, \cdots, X_n$ 为来自标准正态总体 $X$ 的简单随机样本, 记 $\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$, $S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2, T=\bar{X}-S$, 则 $E\left(T^2\right)=$
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $f^{\prime}(x)=\frac{1}{\sqrt{1+x^2}}, g^{\prime}(x)=\frac{1}{1+2 x}$, 且 $f(0)=g(0)=0$, 试求 $\lim _{x \rightarrow 0}\left[\frac{1}{f(x)}-\frac{1}{g(x)}\right]$.
讨论方程 $\frac{1}{x}-\frac{1}{\mathrm{e}^x-1}=a$ 在 $(-\infty, 0)$ 与 $(0,+\infty)$ 内根的个数.
求 $x=\cos t(0 < t < \pi)$ 将方程 $\left(1-x^2\right) y^{\prime \prime}-x y^{\prime}+y=0$ 化为 $y$ 关于 $t$ 的微分方程, 并求满足 $\left.y\right|_{x=0}=1,\left.y^{\prime}\right|_{x=0}=2$ 的解.
计算曲面积分
$$
I=\iint_{\Sigma} 2(1-x y) \mathrm{d} y \mathrm{~d} z+(x+1) y \mathrm{~d} z \mathrm{~d} x-4 y z^2 \mathrm{~d} x \mathrm{~d} y,
$$
其中 $\Sigma$ 是弧段 $\left\{\begin{array}{l}z=\sqrt{x-1}, \\ y=0\end{array},(1 \leqslant x \leqslant 3)\right.$ 绕 $x$ 轴旋转一周所得的旋转曲面, $\Sigma$ 上任一点的法向量与 $x$ 轴正向夹角大于 $\frac{\pi}{2}$.
设二次型 $f\left(x_1, x_2, x_3\right)=\left(x_1-2 x_2\right)^2+\left(x_2-x_3\right)^2+\left(x_1+a x_3\right)^2$.
(1) 求 $f\left(x_1, x_2, x_3\right)=0$ 的解;
(2) 设二次型 $f\left(x_1, x_2, x_3\right)$ 的规范形为 $z_1^2+z_2^2$, 求正交变换 $x=Q y$, 使得二次型 $f\left(x_1, x_2, x_3\right)$ 化为标准形.
设总体 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{ll}2(x-\theta) \mathrm{e}^{-(x-\theta)^2}, & x>\theta, \\ 0, & x \leqslant \theta,\end{array}\left(X_1, X_2, \cdots, X_n\right)\right.$ 为来自总体 $X$ 的简单随机样本.
(1) 求参数 $\theta$ 的矩估计量;
(2) 设 $U=\min \left\{X_1, X_2, \cdots, X_n\right\}$, 求 $E(U)$.
求极限
$$
\lim _{x \rightarrow 0}\left(\frac{-\cot x}{\mathrm{e}^{-x}}+\frac{1}{\mathrm{e}^{-2 x} \sin ^2 x}+\frac{1}{x^2}\right)
$$