圆柱形弹簧的劲度系数 $k$ 与弹簧处于原长时的长度 $L$ 、横截面积 $S$ 有关, 理论与实践都表明 $k=Y \frac{S}{L}$, 其中 $Y$ 是一个由材料决定的常数, 材料学上称之为杨氏模量. 在国际单位制中, 杨氏模量 $Y$ 的单位可表示为

根据海水中的盐分高低可将海水分成不同密度的区域, 当潜艇从海水高密度区域驶人低密度区域, 浮力顿减, 称之为 “掉深”, 如图甲所示, 我国南海舰队某潜艇在高密度海水区域沿水平方向缓慢航行. $t=0$ 时, 该潜艇 “掉深”, 随后采取措施自救脱险, 在 $0 \sim 50 \mathrm{~s}$ 内潜艇竖直方向的 $v-t$ 图像如图乙所示 (设坚直向下为正方向). 不计水的粘滞阻力, 则

如图所示, 一半圆形光滑圆环固定在坚直平面内, $O$ 为圆心, $P$ 为圆环最高点. 中间有孔、质量为 $m$ 的小球穿在圆环上, 轻弹簧一端固定在 $P$ 点, 另一端与小球相连, 小球在 $M$ 点保持静止, $O M$ 与 $O P$ 夹角为 $\theta=60^{\circ}$. 已知重力加速度为 $g$, 则

如图所示, 压缩机通过光滑活塞在汽缸内往复运动来压缩气体, 活塞的中心 $A$ 与转轮在同一平面内, $O$ 为转轮圆心, $B$ 为转轮边缘上一点, $A 、 B$ 处通过较链连接在轻杆两端, 转轮绕 $O$ 点做角速度为 $\omega$ 的匀速圆周运动. 已知转轮半径为 $r$, 则当 $B$ 点从 $O$ 点水平右侧转动到 $O$ 点水平左侧的过程中

某实验小组用数字传感器探究橡皮筋的弹性规律, 实验过程中先缓慢拉长橡皮筋, 然后逐渐恢复至原长, 记录实验数据后, 以橡皮筋的形变量 $\Delta x$ 为横坐标, 橡皮筋的弹力 $F$ 为纵坐标建立直角坐标系, 如图所示, 对应 $O \rightarrow A \rightarrow B \rightarrow C \rightarrow O$ 的过程. 下列判断正确的是

图甲为某游乐园䭒风飞椅, 图乙为其结构示意图, 两个圆雉摆的摆线与坚直方向的夹角分别为 $53^{\circ} 、 37^{\circ}$, 轨迹圆的半径相等, 其中摆球 $A 、 B$ 均视为质点, $\sin 37^{\circ}=0.6 、 \cos 37^{\circ}=0.8$, 下列说法正确的是

图甲为土星探测器拍摄的照片 (图乙为其示意图), 土卫三十五号位于土星内环和外环之间的缝隙里, 由于其对所经过区域的引力作用, 原本平滑的土星环边沿泛起 “涟渏”. 已知两土星环由大量碎块组成且绕土星运行方向相同, 土卫三十五号轨道与两土星环始终位于同一平面,根据图乙中的信息,下列说法正确的是

质量为 $M$ 的粗糛长木板 $a e$ 放在光滑水平面上, $b 、 c 、 d$ 是 $a e$ 的四等分点. 质量为 $m$ 的物块 (可视为质点) 以一定的初速度从 $a$ 点水平滑上木板左端, 经过一段时间物块停在木板上. 上图是物块刚滑上木板时的物块与木板的位置状态,下图是物块刚与木板达到共同速度时的位置.关于木板与物块的质量关系, 可能正确的是

某无人驾驶汽车某次在试驾中的启动过程中以恒定加速度启动, 达到发动机额定功率后继续加速一段时间, 直到达到稳定速度, 汽车所受阻力恒定. $P$ 为发动机功率, $F$ 为牵引力, $v$ 为汽车速度, 下列图像中能正确描述该过程的是

在进行滑雪赛道创新设计中,一位同学设计如图所示的模型, 并用小球替代滑雪运动员进行研究. 该模型滑道由弧形轨道 $E D$ 、水平轨道 $D A$ 、半径为 $R=0.4 \mathrm{~m}$ 的圆弧轨道 $A B$ $\left(\angle A O B=30^{\circ}\right)$ 、足够长的倾斜直轨道 $B C$ 组成, 所有轨道均光滑且平滑连接, 并固定在坚直平面内. 当小球从 $D$ 的左侧弧形轨道上 $P$ 点 (图中未画出) 静止释放后, 不计空气阻力, 则下列表述符合实际情况的是

风能是一种取之不尽用之不竭的清洁能源, 如图所示为利用风能发电的风力发电机, 它的叶片转动时可形成半径为 $R=15 \mathrm{~m}$ 的圆面. 某段时间内该区域的风速大小为 $v=4 \mathrm{~m} / \mathrm{s}$, 凤恰好与叶片转动的圆面垂直, 已知空气的密度为 $\rho=$ $1.2 \mathrm{~kg} / \mathrm{m}^3$, 此风力发电机的发电效率为 $20 \%$, 下列说法正确的是

把一根匀质铁链水平拉直, 沿 $A B$ 方向一部分放在顺时针匀速转动的水平传送带上,一部分放在光滑水平桌面上, 桌面和传送带在 $A$ 点平滑相接 (忽略衔接处空隙), 由于传送带摩擦力的作用, 铁链向右做直线运动, 传送带长度大于铁链长度. $x$ 为铁链在 $A$ 点右侧的长度, $f$为传送带对铁链的摩擦力, $a$ 为铁链的加速度, $F$ 为 $A$ 点右侧铁链对 $A$ 点左侧铁链的拉力, $E_{\mathrm{k}}$ 为铁链的动能, 则在铁链加速进人传送带的过程中, 下列图像可能正确的是

某物理兴趣小组要验证机械能守恒定律, 实验设计方案如图所示, 用轻质细线拴接一小球 (可视为质点), 在悬点 $O$ 的正下方 $B$ 点放置一电热丝, 当悬线摆至电热丝处时立即被烧断, 小球从 $B$ 点做平抛运动落到水平面 $M N$ 上的 $C$ 点, $O$ 点是 $O 、 B$ 点在水平面上的射影, 在 $O B$ 的左侧安装一个量角器, 可以测量释放小球时悬线与坚直方向的夹角 $\alpha, B 、 O$ 两点间的高度差为 $h$, 摆线在运动的过程中与量角器之间没有摩擦, 重力加速度为 $g$, 回答下列问题:
(1) 为完成实验, 还需测量的物理量有 ________ (填字母).
A. 悬线的长度 $L$
B. 小球的质量 $m$
C. $O^{\prime} 、 C$ 两点间的距离 $x$
(2) 若小球在从 $A$ 到 $B$ 的过程中机械能守恒, 则应满足的表达式为 (用已知物理量和所选物理量的字母表示). ________

某同学在实验室取两个完全相同的木盒, 来测量木盒与木板之间的动摩擦因数. 由于实验室中的天平损坏, 无法称量质量, 他采用 “对调法” 完成测量, 如图甲所示, 一端装有定滑轮的长木板固定在水平桌面上,木盒 1 放置在长木板上, 左端与穿过打点计时器的纸带相连, 右端用细线跨过定滑轮与木盒 2 相接.


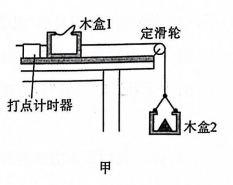
(1) 实验前, ________ (填 “需要” 或 “不需要”) 调整定滑轮的角度使细线与木板平行, (填“需要”或“不需要”) 将长木板左侧垫高来平衡摩擦力.
(2) 实验时, 木盒 1 不放细沙, 在木盒 2 中装人适量的细沙, 接通电源, 释放纸带, 打点计时器打出一条纸带, 加速度记为 $a_1$, 随后将木盒 1 与木盒 2 (含细沙) 位置互换, 换一条纸带再次实验, 打出第二条纸带, 加速度记为 $a_2$, 两纸带编号为第一组, 改变木盒 2 中细沙的多少, 重复上述过程, 得到多组纸带. 如图乙为某组实验中获得的两条纸带中的一条, 其中相邻两计数点间还有 4 个计时点未标出, 已知交流电源的频率为 $50 \mathrm{~Hz}$, 则该纸带运动的加速度 $a=$ ________ $\mathrm{m} / \mathrm{s}^2$ (保留 3 位有效数字).


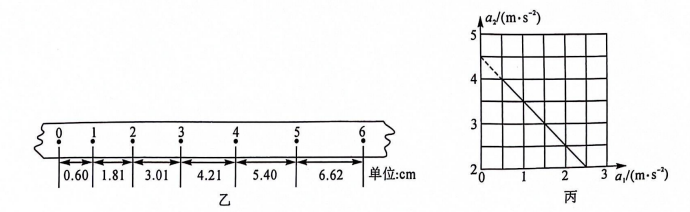
(3) 将实验测得的加速度绘制在丙图中, 得到 $a_2-a_1$ 关系图像, 已知当地重力加速度为 $9.80 \mathrm{~m} / \mathrm{s}^2$, 由图像可得木盒与木板间的动摩擦因数为 ________ (保留 2 位有效数字).
(4) 由于纸带的影响, 实验测得的动摩擦因数将 ________ (填“偏大”或“偏小”).
(5)实验过程中, 有时“对调法”两次实验不能全部完成, 导致实验数据无效,下列能解决此问题的实验方案是 ________ (填字母).
A. 逐步减少木盒 2 的细沙开展后续实验
B. 逐步增多木盒 2 的细沙开展后续实验
C. 开始时直接将细沙放人木盒 1 中开展实验
D. 用密度更大的铁砂代替细沙开展实验

美国航天局的“机智” 号直升机在火星表面尝试动力飞行, 并且在起飞后成功着陆,这是人类首次用飞行器探测其他天体表面. 当“机智”号悬停在空中时, 直升机旋翼提供的动力为 $F$, 已知 “机智” 号的质量为 $m$, 火星的半径为 $R$, 万有引力常量为 $G$, 忽略火星自转的影响. 求:
(1) 火星表面的重力加速度以及火星的质量;
(2) 火星的第一宇宙速度.

如图所示, 在同一坚直平面内固定两个内壁光滑的圆弧轨道 $A B$ 与 $C D E P$, 两轨道在 $B 、 C$ 两点交错对接, $O_1 、 O_2$ 分别是两个轨道的圆心, $O_1 A 、 O_2 E$ 是水平半径, $P O_2 D$ 是坚直直径, 圆弧轨道 $C D E P$ 的半径为 $r, \angle C O_2 P=60^{\circ}$. 现让质量为 $m$ 的小球 (可视为质点) 从 $A$点由静止释放, 沿着圆弧轨道 $A B$ 运动到 $B$ 点后紧接着无碰撞从 $C$ 点进人轨道 $C D E P$, 并沿着轨道运动到 $P$ 点, 小球离开 $P$ 点后刚好到达 $B$ 点 ( $C$ 点), 重力加速度为 $g$, 求:
(1) 小球到达 $P$ 点的速度大小以及轨道 $A B$ 的半径;
(2) 小球第一次到达 $C$ 点时, 轨道 $C E D P$ 对其压力的大小.

如图所示为工业生产中用于定速传输工件的装置模型, 两根半径均为 $R=3 \mathrm{~cm}$ 的相态, 与圆柱间的动摩擦因数 $\mu=0.4$, 两圆柱绕各自的轴线以相同的角速度 $\omega$ 反方向转动. 对钢件施加一个过其重心且平行于圆柱轴线、大小为 $F=16 \mathrm{~N}$ 的拉力. $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$. 求:
(1) 刚施加外力 $F$ 时, 左侧圆柱对钢件的摩擦力 $f_1$ 及钢件的加速度大小 $a$;
(2) 当 $\omega=40 \mathrm{rad} / \mathrm{s}$ 时,钢件可以获得的最大速度 $v_{\mathrm{m}}$;
(3) 为满足不同速度的 “定速传输”, 可改变角速度 $\omega$ 的大小, 试写出 $v_{\mathrm{m}}$ 随 $\omega$ 变化的关系式;
(4) 钢件稳定运动时, 每秒因摩擦产生的热量 $Q$ 和由于传送工件电机多输出的功率 $P$ (角速度 $\omega$ 为某一定值).