单选题 (共 6 题 ),每题只有一个选项正确
2023年4月13日,中国“人造太阳”反应堆中科院环流器装置 创下新纪录,实现403秒稳态长脉冲高约束模等离子体运行,为可控核聚变的最终实现又向前迈出了重要的一步,下列关于核反应的说法正确的是
$\text{A.}$ 相同质量的核燃料,轻核聚变比重核裂变释放的核能更多
$\text{B.}$ 氛氛核聚变的核反应方程为 ${ }_1^2 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}+{ }_{-1}^0 \mathrm{e}$
$\text{C.}$ 核聚变的核反应燃料主要是铀235
$\text{D.}$ 核聚变反应过程中没有质量亏损
如图 (a), 我国某些农村地区人们用手抛撒谷粒进行水稻播种。某次抛出的谷粒中 有两颗的运动轨迹如图 (b) 所示, 其轨迹在同一坚直平面内, 抛出点均为 $O$, 且轨迹 交于 $P$ 点, 抛出时谷粒 1 和谷粒 2 的初速度分别为 $v_1$ 和 $v_2$, 其中 $v_1$ 方向水平, $v_2$ 方向斜 向上。忽略空气阻力, 关于两谷粒在空中的运动, 下列说法正确的是
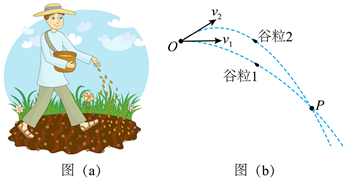
$\text{A.}$ 谷粒 1 的加速度小于谷粒 2 的加速度
$\text{B.}$ 谷粒 2 在最高点的速度小于 $v_1$
$\text{C.}$ 两谷粒从 $O$ 到 $P$ 的运动时间相等
$\text{D.}$ 两谷粒从 $O$ 到 $P$ 的平均速度相等
如图 (a), 在均匀介质中有 $A 、 B 、 C$ 和 $D$ 四点, 其中 $A 、 B 、 C$ 三点位于同一直线上, $A C=B C=4 \mathrm{~m}, D C=3 \mathrm{~m}, D C$ 垂直 $A B . t=0$ 时, 位于 $A 、 B 、 C$ 处的三个完全相同的横 波波源同时开始振动, 振动图像均如图 (b) 所示, 振动方向与平面 $A B D$ 垂直, 已知波 长为 $4 \mathrm{~m}$. 下列说法正确的是
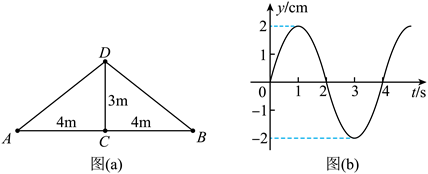
$\text{A.}$ 这三列波的波速均为 $2 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ $t=2 \mathrm{~s}$ 时, $D$ 处的质点开始振动
$\text{C.}$ $t=4.5 \mathrm{~s}$ 时, $D$ 处的质点向 $y$ 轴负方向运动
$\text{D.}$ $t=6 \mathrm{~s}$ 时, $D$ 处的质点与平衡位置的距离是 $6 \mathrm{~cm}$
根据宇宙大爆炸理论, 密度较大区域的物质在万有引力作用下, 不断聚集可能形成 恒星。恒星最终的归宿与其质量有关, 如果质量为太阳质量的 $1 \sim 8$ 㜔将坍缩成白矮星, 质量为太阳质量的 $10 \sim 20$ 㜔将坍缩成中子星, 质量更大的恒星将坍缩成黑洞。设恒星 坞缩前后可看成质量均匀分布的球体, 质量不变, 体积缩小, 自转变快. 不考虑恒星与 其它物体的相互作用. 已知逃逸速度为第一宇宙速度的 $\sqrt{2}$ 傹, 中子星密度大于白矮星。 根据万有引力理论, 下列说法正确的是
$\text{A.}$ 同一恒星表面任意位置的重力加速度相同
$\text{B.}$ 恒星坍缩后表面两极处的重力加速度比坍缩前的大
$\text{C.}$ 恒星坍缩前后的第一宇宙速度不变
$\text{D.}$ 中子星的逃逸速度小于白矮星的逃逸速度
如图, 真空中有三个点电荷固定在同一直线上, 电荷量分别为 $Q_1 、 Q_2$ 和 $Q_3, P$ 点和
三个点电荷的连线与点电荷所在直线的夹角分别为 $90^{\circ} 、 60^{\circ} 、$ 和 $30^{\circ}$ 。若 $P$ 点处的电场 强度为零, $q>0$, 则三个点电荷的电荷量可能为
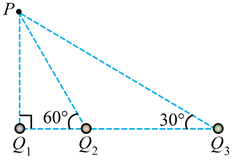
$\text{A.}$ $Q_1=q, Q_2=\sqrt{2} q, Q_3=q$
$\text{B.}$ $Q_1=-q, Q_2=-\frac{4 \sqrt{3}}{3} q, Q_3=-4 q$
$\text{C.}$ $Q_1=-q, Q_2=\sqrt{2} q, Q_3=-q$
$\text{D.}$ $Q_1=q, Q_2=-\frac{4 \sqrt{3}}{3} q, Q_3=4 q$
如图, 真空中有区域I和II, 区域I中存在匀强电场和匀强磁场, 电场方向坚直向下 (与 纸面平行), 磁场方向垂直纸面向里, 等腰直角三角形 $C G F$ 区域 (区域II) 内存在匀强 磁场, 磁场方向垂直纸面向外。图中 $A 、 C 、 O$ 三点在同一直线上, $A O$ 与 $G F$ 垂直, 且 与电场和磁场方向均垂直。 $A$ 点处的粒子源持续将比荷一定但速率不同的粒子射入区域 I 中, 只有沿直线 $A C$ 运动的粒子才能进入区域II。若区域I中电场强度大小为 $E 、$ 磁感应 强度大小为 $B_1$, 区域II中磁感应强度大小为 $B_2$, 则粒子从 $C F$ 的中点射出, 它们在区域 II中运动的时间为 $t 0$ 。若改变电场或磁场强弱, 能进入区域I中的粒子在区域II中运动的 时间为 $t$, 不计粒子的重力及粒子之间的相互作用, 下列说法正确的是
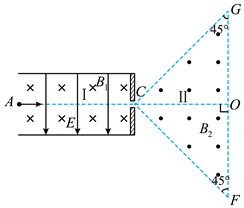
$\text{A.}$ 若仅将区域I中磁感应强度大小变为 $2 B_1$, 则 $t>t_0$
$\text{B.}$ 若仅将区域I中电场强度大小变为 $2 E$, 则 $t>t 0$
$\text{C.}$ 若仅将区域II中磁感应强度大小变为 $\frac{\sqrt{3}}{4} B_2$, 则 $t=\frac{t_0}{2}$
$\text{D.}$ 若仅将区域II中磁感应强度大小变为 $\frac{\sqrt{2}}{4} B_2$, 则 $t=\sqrt{2} t_0$
多选题 (共 4 题 ),每题有多个选项正确
一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是
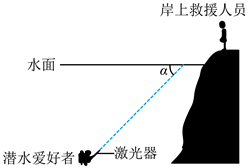
$\text{A.}$ 水的折射率为 $\frac{1}{\sin 41^{\circ}}$
$\text{B.}$ 水的折射率为 $\frac{1}{\sin 49^{\circ}}$
$\text{C.}$ 当他以 $\alpha=60^{\circ}$ 向水面发射激光时, 岸上救援人员接收激光光束的方向与水面夹角小 于 $60^{\circ}$
$\text{D.}$ 当他以 $\alpha=60^{\circ}$ 向水面发射激光时, 岸上救援人员接收激光光束的方向与水面夹角大 于 $60^{\circ}$
如图, 固定在坚直面内的光滑轨道 $A B C$ 由直线段 $A B$ 和圆弧段 $B C$ 组成, 两段相切 于 $B$ 点, $A B$ 段与水平面夹角为 $\theta, B C$ 段圆心为 $O$, 最高点为 $C 、 A$ 与 $C$ 的高度差等于 圆弧轨道的直径 $2 R$ 。小球从 $A$ 点以初速度 $v_0$ 冲上轨道, 能沿轨道运动恰好到达 $C$ 点, 下列说法正确的是
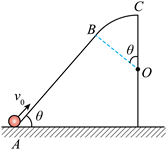
$\text{A.}$ 小球从 $B$ 到 $C$ 的过程中, 对轨道的压力逐渐增大
$\text{B.}$ 小球从 $A$ 到 $C$ 的过程中, 重力的功率始终保持不变
$\text{C.}$ 小球的初速度 $v_0=\sqrt{2 g R}$
$\text{D.}$ 若小球初速度 $v_0$ 增大, 小球有可能从 $B$ 点脱离轨道
某同学自制了一个手摇交流发电机,如图所示。大轮与小轮通过皮带传动(皮带不打滑),半径之比为 ,小轮与线圈固定在同一转轴上。线圈是由漆包线绕制而成的边长为 的正方形,共 匝,总阻值为 。磁体间磁场可视为磁感应强度大小为 的匀强磁场。 大轮以角速度 匀速转动,带动小轮及线圈绕转轴转动,转轴与磁场方向垂直。线圈通过导线、滑环和电刷连接一个阻值恒为 的灯泡。假设发电时灯泡能发光且工作在额定电压以内,下列说法正确的是
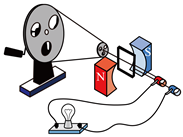
$\text{A.}$ 线圈转动的角速度为 $4 \omega$
$\text{B.}$ 灯泡两端电压有效值为 $3 \sqrt{2} n B L^2 \omega$
$\text{C.}$ 若用总长为原来两倍的相同漆包线重新绕制成边长仍为 $L$ 的多匝正方形线圈, 则灯 泡两端电压有效值为 $\frac{4 \sqrt{2} n B L^2 \omega}{3}$
$\text{D.}$ 若仅将小轮半径变为原来的两倍, 则灯泡变得更亮
如图, 光滑水平地面上有一质量为 $2 m$ 的小车在水平推力 $F$ 的作用下加速运动。车 厢内有质量均为 $m$ 的 $\mathrm{A} 、 \mathrm{~B}$ 两小球, 两球用轻杆相连, $\mathrm{A}$ 球靠在光䫚左壁上, $\mathrm{B}$ 球处在 车厢水平底面上, 且与底面的动摩擦因数为 $\mu$, 杆与坚直方向的夹角为 $\theta$, 杆与车厢始 终保持相对静止假设最大静摩擦力等于滑动摩擦力。下列说法正确的是
$\text{A.}$ 若 B 球受到的摩擦力为零, 则 $F=2 m g \tan \theta$
$\text{B.}$ 若推力 $F$ 向左, 且 $\tan \theta \leq \mu$, 则 $F$ 的最大值为 $2 m g \tan \theta$
$\text{C.}$ 若推力 $F$ 向左, 且 $\mu < \tan \theta \leq 2 \mu$, 则 $F$ 的最大值为 $4 m g(2 \mu-\tan \theta)$
$\text{D.}$ 若推力 $F$ 向右, 且 $\tan \theta>2 \mu$, 则 $F$ 的范围为 $4 m g(\tan \theta-2 \mu) \leq F \leq 4 m g(\tan \theta+2 \mu)$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
某同学探究弹簧振子振动周期与质量的关系,实验装置如图(a)所示,轻质弹簧上端悬挂在铁架台上,下端挂有钩码,钩码下表面吸附一个小磁铁,其正下方放置智能手机,手机中的磁传感器可以采集磁感应强度实时变化的数据并输出图像,实验步骤如下:
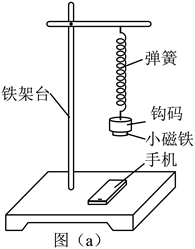
(1) 测出钩码和小磁铁的总质量 $m$;
(2)在弹簧下端挂上该钩码和小磁铁, 使弹簧振子在坚直方向做简谐运动, 打开手机 的磁传感器软件, 此时磁传感器记录的磁感应强度变化周期等于弹簧振子振动周期;
(3) 某次采集到的磁感应强度 $B$ 的大小随时间 $t$ 变化的图像如图 (b) 所示, 从图中可 以算出弹簧振子振动周期 $T=$ (用“ $t_0$ ”表示);

(4)改变钩码质量, 重复上述步骤;
(5) 实验测得数据如下表所示, 分析数据可知, 弹簧振子振动周期的平方与质量的关 系是 (填“线性的”或“非线性的”);

(6) 设弹簧的劲度系数为 $k$, 根据实验结果并结合物理量的单位关系, 弹簧振子振动 周期的表达式可能是 (填正确答案标号);
A. $2 \pi \sqrt{\frac{m}{k}}$
B. $2 \pi \sqrt{\frac{k}{m}}$
C. $2 \pi \sqrt{m k}$
D. $2 \pi k \sqrt{m}$
(7) 除偶然误差外, 写出一条本实验中可能产生误差的原因:
某探究小组利用半导体薄膜压力传感器等元件设计了一个测量微小压力的装置, 其电路 如图 (a) 所示, $R_1 、 R_2 、 R_3$ 为电阻箱, $R_F$ 为半导体薄膜压力传感器, $C 、 D$ 间连接电 压传感器 (内阻无穷大).
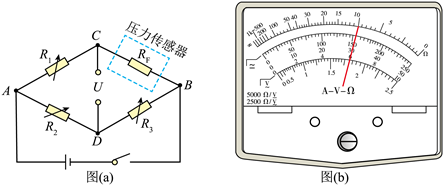
(1) 先用欧姆表“ $\times 100$ ”挡粗测 $R_F$ 的阻值, 示数如图 (b) 所示, 对应的读数是 $\Omega ;$
(2) 适当调节 $R_1 、 R_2 、 R_3$, 使电压传感器示数为 0 , 此时, $R_F$ 的阻值为 (用 $R_1 、 R_2 、 R_3$ 表示);
(3) 依次将 $0.5 \mathrm{~g}$ 的标准砝码加载到压力传感器上(压力传感器上所受压力大小等于砝 码重力大小), 读出电压传感器示数 $U$, 所测数据如下表所示:
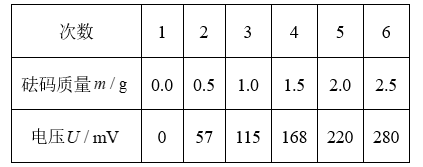
根据表中数据在图(c)上描点,绘制 $U-m$ 关系图线
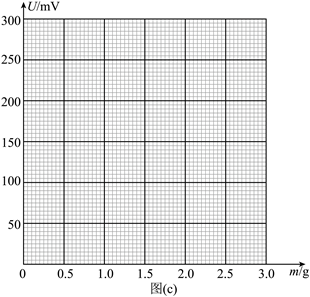
(4)完成前面三步的实验工作后, 该测量微小压力的装置即可投入使用. 在半导体薄 膜压力传感器上施加微小压力 $F_0$, 电压传感器示数为 $200 \mathrm{mV}$, 则 $F_0$ 大小是 $\mathrm{N}$ (重 力加速度取 $9.8 \mathrm{~m} / \mathrm{s}^2$, 保留 2 位有效数字);
(5) 若在步骤 (4) 中换用非理想毫伏表测量 $C 、 D$ 间电压, 在半导体薄膜压力传感器 上施加微小压力 $F_1$, 此时非理想毫伏表读数为 $200 \mathrm{mV}$, 则 $F_1$ $F_0$ (填“>”"="或“ < ”).
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
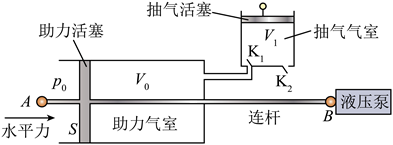
汽车刹车助力装置能有效为驾驶员踩刹车省力. 如图, 刹车助力装置可简化为助力气室 和抽气气室等部分构成, 连杆 $A B$ 与助力活塞固定为一体, 驾驶员踩刹车时, 在连杆 $A B$ 上施加水平力推动液压㶪实现刹车. 助力气室与抽气气室用细管连接, 通过抽气降低助 力气至压强, 利用大气压与助力气室的压强差实现刹车助力. 每次抽气时, $K_1$ 打开, $K_2$ 闭合, 抽气活塞在外力作用下从抽气气室最下端向上运动, 助力气室中的气体充满抽气 气室, 达到两气室压强相等; 然后, $K_1$ 闭合, $K_2$ 打开, 抽气活塞向下运动, 抽气气室 中的全部气体从 $K_2$ 排出, 完成一次抽气过程. 已知助力气室容积为 $V_0$, 初始压强等于 外部大气压强 $p_0$, 助力活塞横截面积为 $\mathrm{S}$, 抽气气室的容积为 $V_1$ 。假设抽气过程中, 助 力活塞保持不动, 气体可视为理想气体, 温度保持不变。
(1) 求第 1 次抽气之后助力气室内的压强 $p_1$;
(2) 第 $n$ 次抽气后, 求该刹车助力装置为驾驶员省力的大小 $\Delta F$ 。
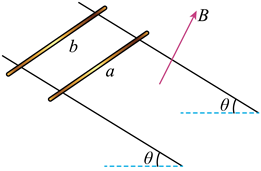
如图, 两根足够长的光滑金属直导轨平行放置, 导轨间距为 $L$, 两导轨及其所构成的平 面均与水平面成 $\theta$ 角, 整个装置处于垂直于导轨平面斜向上的匀强磁场中, 磁感应强度 大小为 $B$. 现将质量均为 $m$ 的金属棒 $a 、 b$ 垂直导轨放置, 每根金属棒接入导轨之间的 电阻均为 $R$ 。运动过程中金属棒与导轨始终垂直且接触良好, 金属棒始终末滑出导轨, 导轨电阻忽略不计, 重力加速度为 $g$ 。
(1) 先保持棒 $b$ 静止, 将棒 $a$ 由静止释放, 求棒 $a$ 匀速运动时的速度大小 $v_0$;
(2) 在 (1) 问中, 当棒 $a$ 匀速运动时, 再将棒 $b$ 由静止释放, 求释放瞬间棒 $b$ 的加速 度大小 $a_0$;
(3) 在 (2) 问中, 从棒 $b$ 释放僢间开始计时, 经过时间 $t_0$, 两棒恰好达到相同的速度 $v$, 求速度 $v$ 的大小, 以及时间 $t_0$ 内榛 $a$ 相对于棒 $b$ 运动的距离 $\Delta \mathrm{x}$ 。
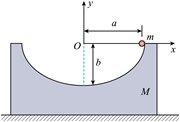
如图, 质量为 $M$ 的匀质凹槽放在光滑水平地面上, 凹槽内有一个半椭圆形的光滑轨道,
椭圆的半长轴和半短轴分别为 $a$ 和 $b$, 长轴水平, 短轴坚直. 质量为 $m$ 的小球, 初始时 刻从椭圆轨道长轴的右端点由静止开始下滑. 以初始时刻椭圆中心的位置为坐标原点, 在坚直平面内建立固定于地面的直角坐标系 $x O y$, 粗圆长轴位于 $x$ 轴上。整个过程凹槽 不翻转, 重力加速度为 $g$ 。
(1) 小球第一次运动到轨道最低点时, 求凹槽的速度大小以及凹槽相对于初始时刻运 动的距离;
(2) 在平面直角坐标系 $x O y$ 中, 求出小球运动的轨迹方程;
(3) 若 $\frac{M}{m}=\frac{b}{a-b}$, 求小球下降 $h=\frac{b}{2}$ 高度时, 小球相对于地面的速度大小 (结果用 $a 、 b$ 及 $g$ 表示)。