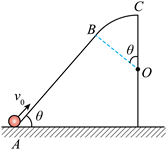
如图, 固定在坚直面内的光滑轨道 $A B C$ 由直线段 $A B$ 和圆弧段 $B C$ 组成, 两段相切 于 $B$ 点, $A B$ 段与水平面夹角为 $\theta, B C$ 段圆心为 $O$, 最高点为 $C 、 A$ 与 $C$ 的高度差等于 圆弧轨道的直径 $2 R$ 。小球从 $A$ 点以初速度 $v_0$ 冲上轨道, 能沿轨道运动恰好到达 $C$ 点, 下列说法正确的是

A. 小球从 $B$ 到 $C$ 的过程中, 对轨道的压力逐渐增大
B. 小球从 $A$ 到 $C$ 的过程中, 重力的功率始终保持不变
C. 小球的初速度 $v_0=\sqrt{2 g R}$
D. 若小球初速度 $v_0$ 增大, 小球有可能从 $B$ 点脱离轨道