科数网
题号:7921    题型:多选题    来源:2023年高考湖南卷物理真题
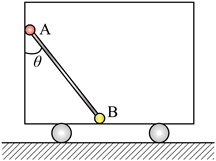
如图, 光滑水平地面上有一质量为 2m 的小车在水平推力 F 的作用下加速运动。车 厢内有质量均为 m 的 A、 B 两小球, 两球用轻杆相连, A 球靠在光䫚左壁上, B 球处在 车厢水平底面上, 且与底面的动摩擦因数为 μ, 杆与坚直方向的夹角为 θ, 杆与车厢始 终保持相对静止假设最大静摩擦力等于滑动摩擦力。下列说法正确的是
A. 若 B 球受到的摩擦力为零, 则 F=2mgtan⁡θ B. 若推力 F 向左, 且 tan⁡θ≤μ, 则 F 的最大值为 2mgtan⁡θ C. 若推力 F 向左, 且 μ<tan⁡θ≤2μ, 则 F 的最大值为 4mg(2μ−tan⁡θ) D. 若推力 F 向右, 且 tan⁡θ>2μ, 则 F 的范围为 4mg(tan⁡θ−2μ)≤F≤4mg(tan⁡θ+2μ)
答案与解析：
答案仅限会员可见 微信内自动登录 或 手机登录 或 微信扫码注册登录 点击我要 开通VIP