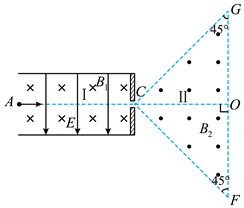
如图, 真空中有区域I和II, 区域I中存在匀强电场和匀强磁场, 电场方向坚直向下 (与 纸面平行), 磁场方向垂直纸面向里, 等腰直角三角形 $C G F$ 区域 (区域II) 内存在匀强 磁场, 磁场方向垂直纸面向外。图中 $A 、 C 、 O$ 三点在同一直线上, $A O$ 与 $G F$ 垂直, 且 与电场和磁场方向均垂直。 $A$ 点处的粒子源持续将比荷一定但速率不同的粒子射入区域 I 中, 只有沿直线 $A C$ 运动的粒子才能进入区域II。若区域I中电场强度大小为 $E 、$ 磁感应 强度大小为 $B_1$, 区域II中磁感应强度大小为 $B_2$, 则粒子从 $C F$ 的中点射出, 它们在区域 II中运动的时间为 $t 0$ 。若改变电场或磁场强弱, 能进入区域I中的粒子在区域II中运动的 时间为 $t$, 不计粒子的重力及粒子之间的相互作用, 下列说法正确的是

A. 若仅将区域I中磁感应强度大小变为 $2 B_1$, 则 $t>t_0$
B. 若仅将区域I中电场强度大小变为 $2 E$, 则 $t>t 0$
C. 若仅将区域II中磁感应强度大小变为 $\frac{\sqrt{3}}{4} B_2$, 则 $t=\frac{t_0}{2}$
D. 若仅将区域II中磁感应强度大小变为 $\frac{\sqrt{2}}{4} B_2$, 则 $t=\sqrt{2} t_0$