单选题 (共 5 题 ),每题只有一个选项正确
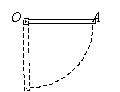
均匀细棒 $\mathrm{OA}$ 可绕通过其一端 $\mathrm{O}$ 而与棒垂直的水平固定光滑轴转动, 如图所示. 今使棒从水平位置由静止开始自由下 落, 在棒摆动到坚直位置的过程中, 下述说法正确的是
$\text{A.}$ 角速度从小到大, 角加速度从大到小
$\text{B.}$ 角速度从小到大, 角加速度从小到大
$\text{C.}$ 角速度从大到小, 角加速度从大到小
$\text{D.}$ 角速度从大到小, 角加速度从小到大
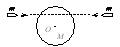
一圆盘正绕垂直于盘面的水平光滑固定轴O转动,如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度将
$\text{A.}$ 增大
$\text{B.}$ 不变
$\text{C.}$ 减小
$\text{D.}$ 不能确定
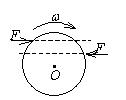
一圆盘绕过盘心且与盘面垂直的光滑固定轴O以角速度w按图示方向转动.若如图所示的情况那样,将两个大小相等方向相反但不在同一条直线的力F沿盘面同时作用到圆盘上,则圆盘的角速度将
$\text{A.}$ 必然增大
$\text{B.}$ 必然减少
$\text{C.}$ 不会改变
$\text{D.}$ 不能确定
将细绳绕在一个具有水平光滑轴的飞轮边缘上, 现在在绳端挂一质量为 $\mathrm{m}$ 的重物, 飞轮的角加速度为 $\beta$. 如果以拉 力 $2 \mathrm{mg}$ 代替重物拉绳时, 飞轮的角加速度将
$\text{A.}$ 小于 $\beta$
$\text{B.}$ 大于 $\beta$, 小于 $2 \beta$
$\text{C.}$ 大于 $2 \beta$
$\text{D.}$ 等于 $2 \beta$
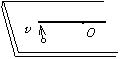
光滑的水平桌面上有长为 $2 l$ 、质量为 $\mathrm{m}$ 的匀质细杆, 可绕通过其中点 $\mathrm{O}$ 且垂直于桌面的坚直固定轴自由转动, 转动惯 量为 $\frac{1}{3} m l^2$, 图所示. 当小球与杆端发生碰撞后, 就与杆粘在一起随杆转动. 则这一系统碰撞后的转动角速度
$\text{A.}$ $\frac{l y}{12}$
$\text{B.}$ $\frac{2 v}{3 l}$
$\text{C.}$ $\frac{3 t}{4 l}$
$\text{D.}$ $\frac{3 \mathrm{t}}{l}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
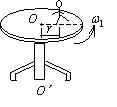
有一半径为 $R$ 的匀质圆形水平转台, 可绕通过盘心 $O$ 且垂直于盘面的坚直固定轴 $O O^{\prime}$ 转动, 转动惯量为 $\mathrm{J}$. 台上有一 人, 质量为 $\mathrm{m}$. 当他站在离转轴 $\mathrm{r}$ 处时 $(\mathrm{r} < \mathrm{R})$, 转台和人一起以 $\omega_1$ 的角速度转动, 如图. 若转轴处摩擦可以忽略, 问当 人走到转台边缘时, 转台和人一起转动的角速度 $\omega_2=$
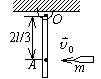
长为 $l$ 、质量为 $\mathrm{M}$ 的包质鿑可绕通过杆一端 $\mathrm{O}$ 的水平光滑固定轴转动, 转动惯量为 $\frac{1}{3} M^2$, 开始时杆坚直下垂, 如图所 示. 有一质量为 $\mathrm{m}$ 的子弹以水平速度 $\vec{v}_0$ 射入杆上 $\mathrm{A}$ 点, 并嵌在杆中, $\mathrm{OA}=2 l / 3$, 则子弹射入后瞬间杆的角速度 $\omega=$
飞轮以 $600 \mathrm{rev} / \mathrm{min}$ 的转速旋转, 转动惯量为 $2.5 \mathrm{~kg} \cdot \mathrm{m}^2$, 现加一恒定的制动力矩使飞轮在 $1 \mathrm{~s}$ 内停止转动, 则该恒定 制动力矩的大小 $\mathrm{M}=$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一长为 $1 \mathrm{~m}$ 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动. 抬起另一端使棒向上与水平面成 $60^{\circ}$, 然后无 $\frac{1}{3} m l^2$
初转速地将棒释放. 已知棒对轴的转动惯量为 $\frac{1}{3} m l^2$, 其中 $\mathrm{m}$ 和 $l$ 分别为棒的质量和长度. 求: (1)放手时棒的角加速 度; (2)棒转到水平位置时的角加速度。

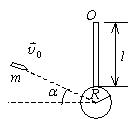
如图所示, 一半径为 $\mathrm{R}$ 的匀质小木球固结在一长度为 $l$ 的匀质细棒的下端, 且可绕水平光滑固定轴 $\mathrm{O}$ 转动. 今有一质量 为 $\mathrm{m}$, 速度为 $\vec{v}_0$ 的子弹, 沿着与水平面成 $\alpha$ 角的方向射向球心, 且嵌于球心. 已知小球、细棒对通过 $\mathrm{O}$ 的水平轴的 转动惯量的总和为 J. 求子弹嵌入球心后系统的共同角速度.
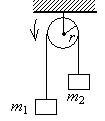
如图所示, 设两重物的质量分别为 $\mathrm{m}_1$ 和 $\mathrm{m}_2$, 且 $\mathrm{m}_1>\mathrm{m}_2$, 定滑轮的半径为 $\mathrm{r}$, 对转轴的转动惯量为 $\mathrm{J}$, 轻绳与滑轮间无滑 动, 滑轮轴上摩擦不计. 设开始时系统静止, 试求 $\mathrm{t}$ 时刻滑轮的角速度.
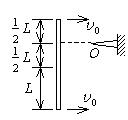
一匀质细棒长为 $2 \mathrm{~L}$, 质量为 $\mathrm{m}$, 以与棒长方向相垂直的速度 $\mathrm{v}_{\mathrm{v}}$ 在光滑水平面内平动时, 与前方一固定的光滑支点 $\mathrm{O}$ 发 生完全非弹性碰撞. 碰撞点位于棒中心的一侧 $\frac{1}{2} L$ 处, 如图所示. 求棒在碰撞后的瞬时绕 $\mathrm{O}$ 点转动的角速度 $\omega$. (细棒 绕通过其端点且与其垂直的轴转动时的转动惯量为 $\frac{1}{3} m l^2$, 式中的 $m$ 和 $l$ 分别为棒的质量和长度.)
一根放在水平光滑桌面上的匀质棒, 可绕通过其一端的坚直固定光滑轴 $\mathrm{O}$ 转动. 棒的质量为 $\mathrm{m}=1.5 \mathrm{~kg}$, 长度为 $l=1.0m$, 对轴的转动惯量为 $\mathrm{J}=\frac{1}{3} m l^2$. 初始时棒静止. 今有一水平运动的子弹垂直地射入棒的另一端, 并留在棒中, 如图所 示. 子弹的质量为 $\mathrm{m}^{\prime}=0.020 \mathrm{~kg}$, 速率为 $\mathrm{v}=400 \mathrm{~m} \cdot \mathrm{s}^{-1}$. 试问:(1)棒开始和子弹一起转动时角速度 $\omega$ 有多大? (2)若棒转动 时受到大小为 $\mathrm{M}=4.0 \mathrm{~N} \cdot \mathrm{m}$ 的恒定阻力矩作用, 棒能转过多大的角度 $\theta ?$
