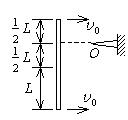
一匀质细棒长为 $2 \mathrm{~L}$, 质量为 $\mathrm{m}$, 以与棒长方向相垂直的速度 $\mathrm{v}_{\mathrm{v}}$ 在光滑水平面内平动时, 与前方一固定的光滑支点 $\mathrm{O}$ 发 生完全非弹性碰撞. 碰撞点位于棒中心的一侧 $\frac{1}{2} L$ 处, 如图所示. 求棒在碰撞后的瞬时绕 $\mathrm{O}$ 点转动的角速度 $\omega$. (细棒 绕通过其端点且与其垂直的轴转动时的转动惯量为 $\frac{1}{3} m l^2$, 式中的 $m$ 和 $l$ 分别为棒的质量和长度.)