单选题 （共 12 题 ），每题只有一个选项正确
实数 -2023 的绝对值是
$\text{A.}$ 2023
$\text{B.}$ -2023
$\text{C.}$ $\frac{1}{2023}$
$\text{D.}$ $-\frac{1}{2023}$
我国倡导的“一带一路”地区覆盖的总人口为 4400000000 人, 这个数用科学记数法表示为
$\text{A.}$ $44 \times 10^8$
$\text{B.}$ $4.4 \times 10^8$
$\text{C.}$ $4.4 \times 10^9$
$\text{D.}$ $44 \times 10^{10}$
下列运算正确的是
$\text{A.}$ $a^3 \cdot a^4=a^{12}$
$\text{B.}$ $\left(a^3\right)^3=a^6$
$\text{C.}$ $a^4 \div a^3=a$
$\text{D.}$ $a^3+a^4=a^7$
某学生6次立定跳远的成绩 (单位 $c m$ ) 如下： $150,160,165,145,150,170$. 下列关于这组数据的描述不正确的是
$\text{A.}$ 众数是 150
$\text{B.}$ 中位数是 155
$\text{C.}$ 极差是 20
$\text{D.}$ 平均数是 $\frac{470}{3}$
不等式组 $\left\{\begin{array}{l}x-1>0, \\ 5-2 x \geq 1\end{array}\right.$ 的解集在数轴上表示正确的是
$\text{A.}$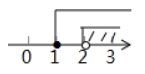 
$\text{B.}$ 
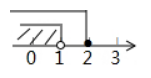$\text{C.}$ 
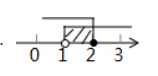$\text{D.}$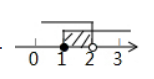 
分式方程 $\frac{1}{x-2}=\frac{3}{x}$ 的解为
$\text{A.}$ $x=3$
$\text{B.}$ $x=2$
$\text{C.}$ $x=1$
$\text{D.}$ 无解
在平面直角坐标系中, 点 $A$ 的坐标为 $A(1,2)$, 点 $A$ 与点 $A^{\prime}$ 关于 $x$ 轴对称, 则点 $A^{\prime}$ 的坐标是
$\text{A.}$ $(-2,1)$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $(-1,-2)$
$\text{D.}$ $(1,-2)$
如图, 已知 $a / / b$, 直角三角板的直角顶点在直线 $a$ 上, 若 $\angle 1=40^{\circ}$, 则 $\angle 2$ 等于
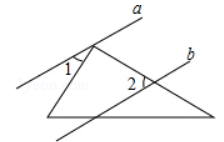
$\text{A.}$ $40^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $70^{\circ}$
如图所示, 在 $\triangle A B C$ 中, $\angle B=55^{\circ}, \angle C=30^{\circ}$, 分别以点 $A$ 和点 $C$ 为圆心, 大于 $\frac{1}{2} A C$ 的长为半 径画弧, 两弧相交于点 $M, N$, 作直线 $M N$, 交 $B C$ 于点 $D$, 连接 $A D$, 则 $\angle B A D$ 的度数为
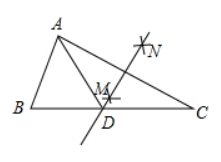
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $55^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $65^{\circ}$
如图, $A B$ 是 $\odot O$ 的直径, 弦 $C D \perp A B$ 于点 $E, \angle B C D=22.5^{\circ}, A B=8$, 则 $C D$ 的长为
$\text{A.}$ $4 \sqrt{3}$
$\text{B.}$ $4 \sqrt{2}$
$\text{C.}$ 4
$\text{D.}$ 6
如图, 反比例函数 $y=\frac{k}{x}(x>0)$ 图象经过正方形 $O A B C$ 的顶点 $A, B C$ 边与 $y$ 轴交于点 $D$, 若 正方形 $O A B C$ 的面积为 $12, B D=2 C D$, 则 $k$ 的值为
$\text{A.}$ 3
$\text{B.}$ $\frac{18}{5}$
$\text{C.}$ $\frac{16}{5}$
$\text{D.}$ $\frac{10}{3}$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
把多项式 $3 x^2-3 y^2$ 因式分解的结果是
已知关于 $x$ 的方程 $x^2+2 x-a=0$ 的一个根为 2 , 则另一个根是
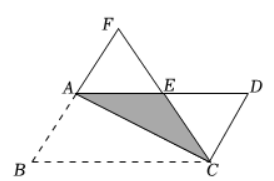
如图, 在平行四边形纸片 $A B C D$ 中, $A B=2 \mathrm{~cm}$, 将纸片沿对角线 $A C$ 对折至 $C F$, 交 $A D$ 边 于点 $E$, 此时 $\triangle B C F$ 恰为等边三角形, 则图中折叠重合部分的面积是
如图, 菱形 $A B C D, A E \perp B C$, 点 $E$ 为垂足, 点 $F$ 为 $A E$ 的中点, 连接 $B F$ 并延长交 $A D$ 于点 $G$, 连接 $C G, C E=2, C G=2 \sqrt{11}$, 则 $D G=, A G=6, A F=$.
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
( 1 ) $2^3 \div \sqrt{4}-|-5|+\left(\frac{1}{3}\right)^{-2}$;
(2) $(a+2)^2-a(a+2)$.
已知二次函数 $y=a x^2+b x+c$ 的图像经过 $A(1,5) 、 B(0,3) 、 C(-1,-3)$ 三点.
(1) 求这个函数的解析式.
( 2 ) 用配方法求出这个二次函数图像的顶点坐标.
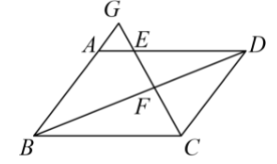
如图，已知在平行四边形 $A B C D$ 中， $E$ 是 $A D$ 边上的一点， $C E$ 与 $B D$ 相交于点 $F ， C E$ 与 $B A$ 的延长线相 交于点 $G ， D E=3 A E ， C E=12$. 求 $G E 、 C F$ 的长.
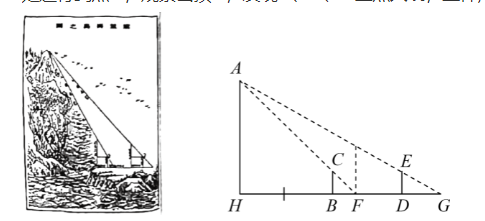
《海岛算经》是中国古代测量术的代表作，原名《重差》. 这本著作建立起了从直接测量向间接测量的 桥梁. 直至近代，重差测量法仍有借鉴意义.
如图，为测量海岛上一座山峰 $A H$ 的高度，直立两根高 2 米的标杆 $B C$ 和 $D E$ ，两杆间距 $B D$ 相距 6 米， $D$ $B 、 H$ 三点共线. 从点 $B$ 处退行到点 $F$ ，观察山顶 $A$ ，发现 $A 、 C 、 F$ 三点共线，且仰角为 $45^{\circ}$ ；从点 $D$ 处退行到点 $G$ ，观察山顶 $A$ ，发现 $A 、 E 、 G$ 三点共线，且仰角为 $30^{\circ}$. (点 $F 、 G$ 都在直线 $H B$ 上)
(1) 求 $F G$ 的长 (结果保留根号).
（2）山峰高度 $A H$ 的长 (结果精确到 0.1 米). (参考数据: $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ )
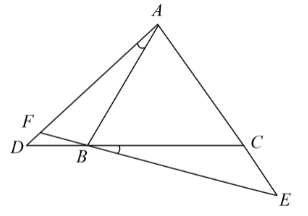
如图，已知在 $\triangle A B C$ 中， $A B=A C$ ，点 $D 、 E$ 分别在边 $C B 、 A C$ 的延长线上，且 $\angle D A B=\angle E B C$ ， $E B$ 的延长线交 $A D$ 于点 $F$.
(1) 求证: $\triangle D B F \sim \triangle E B C$.
(2) 如果 $A B=B C$ ，求证: $E C^2=D F \cdot D A$.
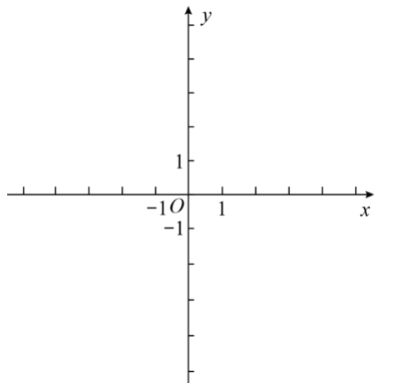
如图，已知在平面直角坐标系 $x O y$ 中，抛物线 $y=x^2+b x+c$ 经过 $A(-1,4) 、 B(3,-4)$ 两点，且与 $y$ 轴 的交点为点 $C$.
( 1 ) 求此抛物线的表达式及对称轴.
(2) 求 $\cot \angle O B C$ 的值.
(3) 在抛物线上是否存在点 $P$ ，使得 $\triangle P B C$ 是以 $B C$ 为直角边的直角三角形? 如果存在，求出所有符 合条件的点 $P$ 坐标；如果不存在，请说明理由.
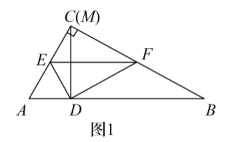
已知Rt $\triangle A B C$ 中， $\angle C=90^{\circ} ， \angle B=30^{\circ} ， A B=4$ ，点 $E 、 F$ 分别在边 $A C 、$ 边 $B C$ 上 (点 $E$ 不与点 $A$ 重合，点 $F$ 不与点 $B$ 重合），联结 $E F$ ，将 $\triangle C E F$ 沿着直线 $E F$ 翻折后，点 $C$ 恰好落在边 $A B$ 上的点 $D$ 处. 过点 $D$ 作 $D M \perp A B$ ，交射线 $A C$ 于点 $M$. 设 $A D=x ， \frac{C F}{C E}=y$ ，
（1）如图 1 ，当点 $M$ 与点 $C$ 重合时，求 $\frac{M D}{E D}$ 的值.
( 2 ) 如图 2 ，当点 $M$ 在线段 $A C$ 上时，求 $y$ 关于 $x$ 的函数解析式，并写出定义域.
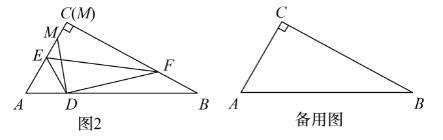
（3）当 $\frac{C M}{C E}=\frac{1}{2}$ 时，求 $A D$ 的长.