已知Rt $\triangle A B C$ 中, $\angle C=90^{\circ} , \angle B=30^{\circ} , A B=4$ ,点 $E 、 F$ 分别在边 $A C 、$ 边 $B C$ 上 (点 $E$ 不与点 $A$ 重合,点 $F$ 不与点 $B$ 重合),联结 $E F$ ,将 $\triangle C E F$ 沿着直线 $E F$ 翻折后,点 $C$ 恰好落在边 $A B$ 上的点 $D$ 处. 过点 $D$ 作 $D M \perp A B$ ,交射线 $A C$ 于点 $M$. 设 $A D=x , \frac{C F}{C E}=y$ ,
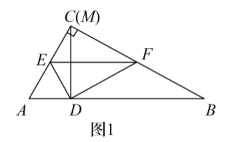
(1)如图 1 ,当点 $M$ 与点 $C$ 重合时,求 $\frac{M D}{E D}$ 的值.
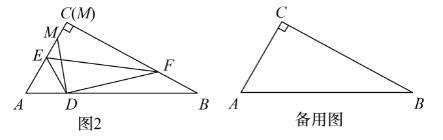
( 2 ) 如图 2 ,当点 $M$ 在线段 $A C$ 上时,求 $y$ 关于 $x$ 的函数解析式,并写出定义域.
(3)当 $\frac{C M}{C E}=\frac{1}{2}$ 时,求 $A D$ 的长.
(1)如图 1 ,当点 $M$ 与点 $C$ 重合时,求 $\frac{M D}{E D}$ 的值.

( 2 ) 如图 2 ,当点 $M$ 在线段 $A C$ 上时,求 $y$ 关于 $x$ 的函数解析式,并写出定义域.

(3)当 $\frac{C M}{C E}=\frac{1}{2}$ 时,求 $A D$ 的长.