单选题 (共 5 题 ),每题只有一个选项正确
如图所示, 实线为一列沿 $x$ 轴正方向传播的简谐横波在 $t=0$ 时刻的波形, 虚线是该机械波在 $t=0.20 \mathrm{~s}$ 时刻的波形, 则此 列波的周期可能为

$\text{A.}$ 0.1s
$\text{B.}$ 0.2s
$\text{C.}$ 0.4s
$\text{D.}$ 0.8s
我国北斗三号使用的氢原子钟是世界上最先进的原子钟。它每天的变化只有十亿分之一秒, 它是利用氢原子吸收或释放能量发出的电磁波来计时的。如图所示为氢原子能级图, 大量处于基态的氢原子吸收某种频率的光子跃迁到激发态后, 只能辐射三种不同频率的光子,能量最大的光子与能量最小的光子的能量差为
$\text{A.}$ $13.6 \mathrm{eV}$
$\text{B.}$ $12.09 \mathrm{eV}$
$\text{C.}$ $10.2 \mathrm{eV}$
$\text{D.}$ $1.89 \mathrm{eV}$
一个物块在光滑的水平面上受到水平恒力 $F$ 的作用, 从静止开始做匀加速直线运动, 计 时开始的 $\frac{x}{t}-t$ 图像如甲所示, $v^2-x$ 图像如图乙所示,据图像的特点与信息分析,下列说 法正确的是
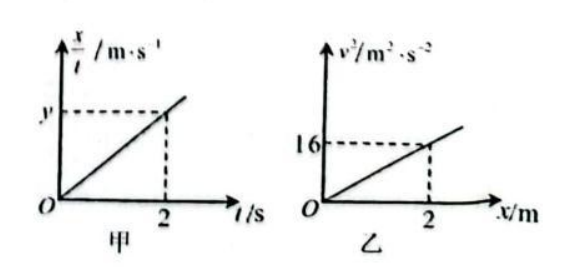
$\text{A.}$ $x=1 \mathrm{~m}$ 时物体的速度为 $8 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ 图乙的斜率是图甲的斜率的 2 倍
$\text{C.}$ 图甲中的 $y=8 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ $t=1 \mathrm{~s}$ 时物体的速度为 $4 \mathrm{~m} / \mathrm{s}$
2022 年 12 月 4 日 20 时 09 分, 神舟十四号载人飞船返回舱在东风着降场成功着陆。 三名航天员安全返回。设神舟十四号飞船的质量为 $m$, 飞船与空间站相对静止, 共同在距地面高为 $h$ 处做匀速圆周运动, 地球半径为 $R$, 地球表面重力加速度为 $g$ 。忽略地球自转. 下列关于神舟十四号飞船在轨运行的说法正确的是
$\text{A.}$ 周期为 $\frac{2 \pi}{R} \sqrt{\frac{h^3}{g}}$
$\text{B.}$ 向心加速度为 $\frac{g R^2}{(R+h)^2}$
$\text{C.}$ 角速度为 $R \sqrt{\frac{g}{R+h}}$
$\text{D.}$ 动能为 $\frac{1}{2} m g R$
如图所示, 水平面上的小车内固定一个倾角为 $\theta=30^{\circ}$ 的光滑斜面 平行于斜面的细绳一端固定在车上, 另一端系着一个质量为 $m$ 的 小球,小球和小车均处于静止状态。如果小车在水平面上向左加 速且加速度大小不超过 $a_1$ 时, 小球佮能和小车保持相对静止; 如 果小车在水平面上向右加速且加速度大小不超过 $a_2$ 时, 小球仍 能够和斜面接触且保持相对静止, 则 $a_1$ 和 $a_2$ 的大小之比为

$\text{A.}$ $1:3$
$\text{B.}$ $\sqrt{3}:3$
$\text{C.}$ $3:1$
$\text{D.}$ $\sqrt{3}:1$
多选题 (共 3 题 ),每题有多个选项正确
如图所示,轻弹簧左端固定, 右端连接物体 $A$, 物体 $A$ 置于光滑水平桌面上, 物体 $A$ 和 $B$ 通过细绳绕过定滑轮连接。已知物体 $A$ 和 $B$ 的质量分别为 $m$ 和 $2 m$, 弹簧的劲度系数为 $k$, 不计滑轮摩摞。物体 $A$ 位于 $O$ 点时, 系统处于共止状态, 物体 $A$ 在 $P$ 点时弹簧处于原 长。现将物体 $A$ 由 $P$ 点静止释放,物体 $A$ 不会和定滑轮相碰,当物体 $B$ 向下运动到最低点时,绳子恰好被拉断且弹共末超过弹性限度, 则
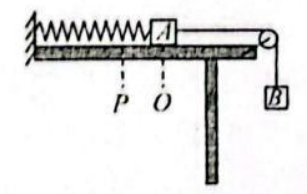
$\text{A.}$ 由 $P$ 点释放物体 $A$ 瞬间,物体 $A$ 的加速度为零
$\text{B.}$ 绳子能承受的最大拉力为 $\frac{10}{3} m g$
$\text{C.}$ 从 $P$ 点到 $O$ 点,物体 $A$ 劫能的增加量小于重力对物体 $B$ 所做功与弹簧弹力对 $A$ 做的 功之和
$\text{D.}$ 从 $P$ 点到 $O$ 点,物体 $A$ 与弹簧所组成的系统机械能的增加量等于物体 $B$ 所受重力对 $B$ 做的功
速度选择器可以使一定速度的粒子沿直线运动, 如图甲 所示。霍尔元件的工作原理与速度选择器类似, 某载流 子为电子的霍尔元件如图乙所示。下列说法正确的是
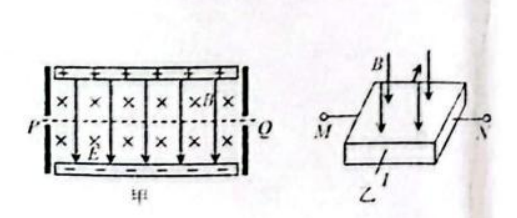
$\text{A.}$ 图甲中, 电子以速度大小 $v=\frac{E}{B}$ 从 $Q$ 端射入, 可沿直线运动从 $P$ 点射出
$\text{B.}$ 图甲中, 电子以速度大小 $v>\frac{E}{B}$ 从 $P$ 端射入, 电子向下偏转,轨迹为抛物线
$\text{C.}$ 图乙中, 仅增大电流 $I$, 其他条件不变, $M N$ 之间的霍尔电压将增大
$\text{D.}$ 图乙中, 稳定时霍尔元件 $M$ 侧的电势低于 $N$ 侧的电势
如图所示, $A 、 B 、 C$ 是等边三角形的三个顶点, $A B$ 边的中点为 $M$, $B C$ 边的中点为 $N, O$ 点为三角形的中心, 分别在 $A 、 B 、 C$ 固定放置 电荷量为 $+Q 、+Q 、-Q$ 的点电荷时, 下列说法正确的是
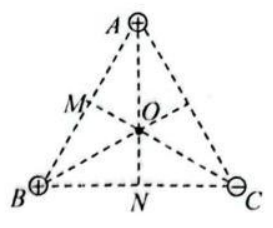
$\text{A.}$ $M, N$ 两点的电场强度大小相等
$\text{B.}$ $M$ 点的电势高于 $N$ 点的电势
$\text{C.}$ 将一个不计重力的负电荷沿直线由 $O$ 点向 $C$ 点移动的过程中, 电势能逐渐减小
$\text{D.}$ 将一个不计重力的负电荷沿直线由 $O$ 点向 $N$ 点移动的过程中, 受到的电场力做负功
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
近年来我国芯片制造方面不断研究, 取得了不少进展。在芯片制造过程中, 粒子注入是其中一道重要的工序,其工作原理的示意图如图所示。静止于 A 的离子,经电压为U的加速电场加速后,沿图中半径为R的虚线通过圆弧形静点分析器(静点分析器通道内有均匀辐向分布的电场)后,从P点沿直径$PQ$方向进入半径也为R的圆柱形、方向垂直于纸面向外的匀强磁场区域,
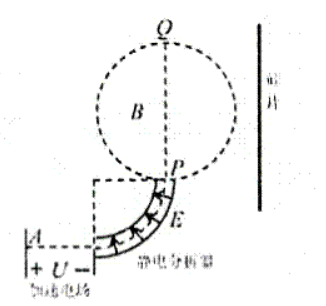
粒子经磁场偏转,最后垂直打在竖直放置的硅片上的M点(图中未画出),已知粒子的质量为m,电荷量为q,不计重力,求
(1) 粒子进入圆形匀强磁场区域是的速度v和静电分析器通道内虚线处电场强度$E$的大小
(2) 匀强磁场的磁感应强度 $B$ 的大小
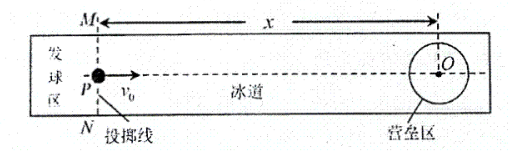
冰壶是冬季奥运会上非常受欢迎的体育项目:如图所示, 运动员在水平冰而上 将冰壶 $A$ 推到 $P$ 点放手, 此时 $\mathrm{A}$ 的速度 $v_0=4 \mathrm{~m} / \mathrm{s}$, 恰好能匀减速滑行距漓 $x=40 \mathrm{~m}$ 到达 $O$点,用毛刷擦冰面,可使冰面的动摩擦因素减小为$\mu_2=0.015$, 为了赢得比赛,需设法将对手禁止在O点的冰壶B撞出营垒区(垒区内只有冰壶B),运动员仍以$v_0$掷出A壶后,在距投掷线某处开始用毛刷擦冰面,最终将B壶撞出了营垒区,一直A,B的质量相同均视为质点, 冰壸均沿直线 $P O$ 运动, 两个冰壶间的碰撞为弹性正碰, 营垒区半径 $R=1.8 \mathrm{~m}$, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 求:
(1) 末用毛刷擦冰面时冰壶与冰面的动摩擦因素数 $\mu_1$;
(2) 运动员用毛刷擦冰面的长度至少为多少?
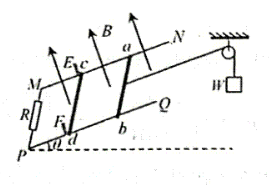
如图所示, 两光滑平行金属导轨 $M N 、 P Q$ 间距为 $L$, 与水平面成 $\theta=30^{\circ}, M P$ 间接 有阻值为 $R$ 的电阻。完全相同的两金属棒 $a b 、 c d$ 垂直导轨放置, 与导轨接触良好。两棒 面向上, 导轨电阻不计。开始时让 $a b 、 c d$ 静止于卡槽 $E F$ 处, 现用轻质绝缘细线一端连接 $a b$, 另一端绕过光滑定滑轮与重物 $W$ 相连, 用手托着重物 $W$ 使细绳伸直且佮无张力。访 手后重物 $W$ 下降的高度为 $x$ 时, $a b$ 棒的速度达到最大, 此时 $c d$ 棒对卡槽 $E F$ 恰好无压26. (20 分) 力。已知重力加速度为 $g$, 在 $a b$ 棒从开始运动 到最大速度的过程中,求:
(1) 重物 $W$ 的质量及 $a b$ 棒的最大速度 $v_{\max }$;
(2) 电阻 $R$ 上产生的焦耳热 $Q_R$ ;
(3) $a b$ 棒运动的时间 $t$.