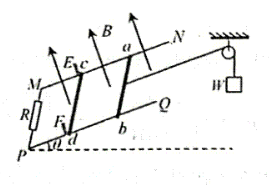
如图所示, 两光滑平行金属导轨 $M N 、 P Q$ 间距为 $L$, 与水平面成 $\theta=30^{\circ}, M P$ 间接 有阻值为 $R$ 的电阻。完全相同的两金属棒 $a b 、 c d$ 垂直导轨放置, 与导轨接触良好。两棒 面向上, 导轨电阻不计。开始时让 $a b 、 c d$ 静止于卡槽 $E F$ 处, 现用轻质绝缘细线一端连接 $a b$, 另一端绕过光滑定滑轮与重物 $W$ 相连, 用手托着重物 $W$ 使细绳伸直且佮无张力。访 手后重物 $W$ 下降的高度为 $x$ 时, $a b$ 棒的速度达到最大, 此时 $c d$ 棒对卡槽 $E F$ 恰好无压26. (20 分) 力。已知重力加速度为 $g$, 在 $a b$ 棒从开始运动 到最大速度的过程中,求:
(1) 重物 $W$ 的质量及 $a b$ 棒的最大速度 $v_{\max }$;
(2) 电阻 $R$ 上产生的焦耳热 $Q_R$ ;
(3) $a b$ 棒运动的时间 $t$.
(1) 重物 $W$ 的质量及 $a b$ 棒的最大速度 $v_{\max }$;
(2) 电阻 $R$ 上产生的焦耳热 $Q_R$ ;
(3) $a b$ 棒运动的时间 $t$.
