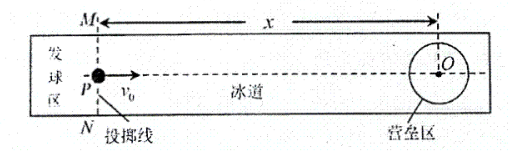
冰壶是冬季奥运会上非常受欢迎的体育项目：如图所示, 运动员在水平冰而上 将冰壶 $A$ 推到 $P$ 点放手, 此时 $\mathrm{A}$ 的速度 $v_0=4 \mathrm{~m} / \mathrm{s}$, 恰好能匀减速滑行距漓 $x=40 \mathrm{~m}$ 到达 $O$点，用毛刷擦冰面，可使冰面的动摩擦因素减小为$\mu_2=0.015$, 为了赢得比赛，需设法将对手禁止在O点的冰壶B撞出营垒区（垒区内只有冰壶B），运动员仍以$v_0$掷出A壶后，在距投掷线某处开始用毛刷擦冰面，最终将B壶撞出了营垒区，一直A,B的质量相同均视为质点, 冰壸均沿直线 $P O$ 运动, 两个冰壶间的碰撞为弹性正碰, 营垒区半径 $R=1.8 \mathrm{~m}$, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 求:
(1) 末用毛刷擦冰面时冰壶与冰面的动摩擦因素数 $\mu_1$;
(2) 运动员用毛刷擦冰面的长度至少为多少?