单选题 （共 12 题 ），每题只有一个选项正确
下列各组数可能是一个三角形的边长的是（）
$\text{A.}$ $4,4,9$
$\text{B.}$ $2,6,8$
$\text{C.}$ $3,4,5$
$\text{D.}$ $1,2,3$
下列图形不具有稳定性的是
$\text{A.}$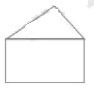 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
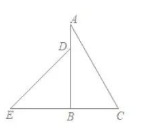
如图, 把一副含 $30^{\circ}$ 角和 $45^{\circ}$ 角的直角三角板拼在一起, 那么图中 $\angle A D E$ 是（）
$\text{A.}$ $100^{\circ}$
$\text{B.}$ $120^{\circ}$
$\text{C.}$ $135^{\circ}$
$\text{D.}$ $150^{\circ}$
一个正多边形, 它的每一个外角都等于 $40^{\circ}$, 则该正多边形是 ( )
$\text{A.}$ 正六边形
$\text{B.}$ 正七边形
$\text{C.}$ 正八边形
$\text{D.}$ 正九边形
如图, $\triangle A B C \cong \triangle B A D$, 点 $A$ 和点 $B$, 点 $C$ 和点 $D$ 是对应点, 如果 $A B=6 \mathrm{~cm}, B D=5 \mathrm{~cm}, A D=4 \mathrm{~cm}$, 那么 $A C$ 的长是
$\text{A.}$ 4cm
$\text{B.}$ 5cm
$\text{C.}$ 6cm
$\text{D.}$ 无法确定
如图, $\triangle A B C$ 和 $\triangle D E F$ 中, $A B=D E 、 \angle B=\angle D E F$, 添加下列哪一个条件无法证明 $\triangle A B C \cong \triangle D E F$
$\text{A.}$ $A C / / D F$
$\text{B.}$ $\angle A=\angle D$
$\text{C.}$ $A C=D F$
$\text{D.}$ $\angle A C B=\angle F$
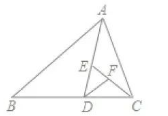
如图, $A D$ 是 $\triangle A B C$ 的中线, $C E$ 是 $\triangle A C D$ 的中线, $D F$ 是 $\triangle C D E$ 的中线, 如果 $\triangle D E F$ 的面积是 2 , 那么 $\triangle A B C$ 的面积为
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 16
$\text{D.}$ 18
如图, 在锐角 $\triangle A B C$ 中, $C D, B E$ 分别是 $A B, A C$ 边上的高, 且 $C D, B E$ 相交于一点 $P$, 若 $\angle A=50^{\circ}$, 则 $\angle B P C=$
$\text{A.}$ $150^{\circ}$
$\text{B.}$ $130^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $100^{\circ}$
已知 $A D$ 是 $\triangle A B C$ 的一条中线, $A B=9, A C=7$, 则 $A D$ 的取值范围是（ )
$\text{A.}$ $7 < A D < 9$
$\text{B.}$ $2 < A D < 16$
$\text{C.}$ $1 < A D < 8$
$\text{D.}$ $7 < A D < 8$
如图, $\angle A O B$ 是一钢架, $\angle A O B=15^{\circ}$, 为使钢架更加牢固, 需在其内部添加一些钢管 $E F 、 F G$ 、 $G H \cdots$ 添的钢管长度都与 $O E$ 相等, 则最多能添加这样的钢管（）根.
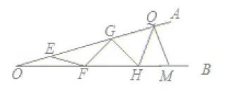
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 无数
如图, 已知线段 $A B=20$ 米, $M A \perp A B$ 于点 $A, M A=6$ 米, 射线 $B D \perp A B$ 于, $P$ 点从 $B$ 点向 $A$ 运动, 每 秒走 1 米, $Q$ 点从 $B$ 点向 $D$ 运动, 每秒走 3 米, $P 、 Q$ 同时从 $B$ 出发, 则出发 $x$ 秒后, 在线段 $M A$ 上有一点 $C$, 使 $\triangle C A P$ 与 $\triangle P B Q$ 全等, 则 $x$ 的值为（）
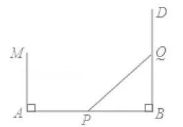
$\text{A.}$ 5
$\text{B.}$ 5或10
$\text{C.}$ 10
$\text{D.}$ 6或10
填空题 （共 6 题 ），请把答案直接填写在答题纸上
已知等腰三角形的两边长是 $5 \mathrm{~cm}$ 和 $11 \mathrm{~cm}$, 则它的周长是
如图, 已知 $A B=B C$, 要使 $\triangle A B D \cong \triangle C B D$, 还需添加一个条件, 你添加的条件 是 . (只需写一个, 不添加輔助线)
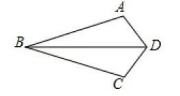
$B M$ 是 $\triangle A B C$ 中 $A C$ 边上的中线, $A B=5 \mathrm{~cm}, B C=3 \mathrm{~cm}$, 那么 $\triangle A B M$ 与 $\triangle B C M$ 的周长之差为 $\mathrm{cm}$
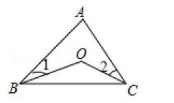
如图, 点 $O$ 是 $\triangle A B C$ 内一点, $\angle A=80^{\circ}, \angle 1=15^{\circ}, \angle 2=40^{\circ}$, 则 $\angle B O C=$
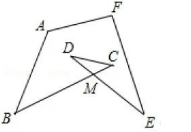
如图, 已知 $B C$ 与 $D E$ 交于点 $M$, 则 $\angle A+\angle B+\angle C+\angle D+\angle E+\angle F$ 的度数为
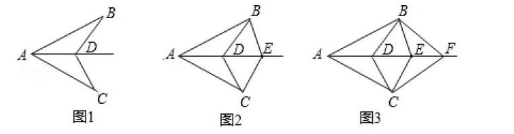
18. 如图, 已知 $A B=A C, D$ 为 $\angle B A C$ 的角平分线上面一点, 连接 $B D, C D$; 如图 2 , 已知 $A B=A C, D$ 、 $E$ 为 $\angle B A C$ 的角平分线上面两点, 连接 $B D, C D, B E, C E$; 如图3, 已知 $A B=A C, D 、 E 、 F$ 为 $\angle$ $B A C$ 的角平分线上面三点, 连接 $B D, C D, B E, C E, B F, C F ; \cdots$, 依次规律, 第 $n$ 个图形中有全等 三角形的对数是
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
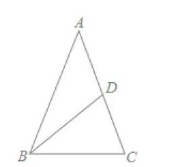
如图, $\triangle A B C$ 中, $\angle A B C=\angle C=70^{\circ}, B D$ 平分 $\angle A B C$, 求 $\angle A D B$ 的度数.
一个正多边形的一个内角的度数比相邻外角的6倍还多 $12^{\circ}$, 求这个正多边形的内角和.
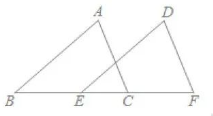
如图, 点 $B 、 E 、 C 、 F$ 在同一条直线上, $A B=D E, A C=D F, B E=C F$, 求证: $A B / / D E$.
如图所示, 在 $\triangle A B C$ 中, $A D$ 是高, $A E 、 B F$ 是角平分线, 它们相交于点 $O, \angle B A C=50^{\circ}, \angle C=$ $70^{\circ}$, 求 $\angle D A C 、 \angle B O A$ 的度数.
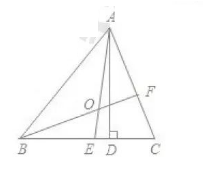
如图, $\triangle A B C$ 中, $A D \perp B C$ 于 $D$, 若 $B D=A D, F D=C D$.
(1) 求证: $\angle F B D=\angle C A D$;
(2) 求证: $B E \perp A C$.
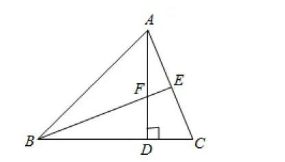
如图, 点 $B$ 在 $A E$ 上, 点 $D$ 在 $A C$ 上, $A B=A D$. 请你添加一个适当的条件, 使 $\triangle A B C \cong \triangle A D E$ (只能 添加一个）.
(1) 你添加的条件是
(2) 添加条件后, 请说明 $\triangle A B C \cong \triangle A D E$ 的理由.
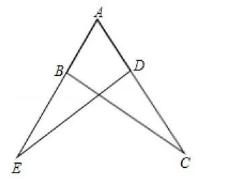
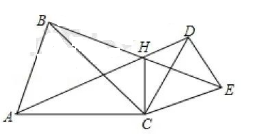
如图, $C A=C B, C D=C E, \angle A C B=\angle D C E=\alpha, A D 、 B E$ 交于点 $H$, 连 $C H$.
(1) 求证: $\triangle A C D \cong \triangle B C E$;
(2) 求证: $H C$ 平分 $\angle A H E$;
(3) 求 $\angle C H E$ 的度数. (用含 $\alpha$ 的式子表示)
