单选题 (共 12 题 ),每题只有一个选项正确
设随机变量 $X_i \sim\left(\begin{array}{ccc}-1 & 0 & 1 \\ \frac{1}{4} & \frac{1}{2} & \frac{1}{4}\end{array}\right)(i=1,2)$, 且满足 $P\left\{X_1 X_2=0\right\}=1$, 则 $P\left\{X_1=\right.$ $\left.X_2\right\}$ 等于
$\text{A.}$ 0.
$\text{B.}$ $\frac{1}{4}$.
$\text{C.}$ $\frac{1}{2}$.
$\text{D.}$ 1 .
二维随机变量 $(X, Y)$ 的概率分布为
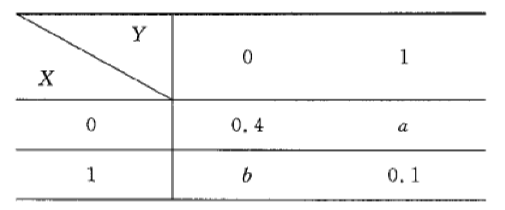
已知随机事件 $\{X=0\}$ 与 $\{X+Y=1\}$ 相互独立, 则
$\text{A.}$ $a=0.2, b=0.3$.
$\text{B.}$ $a=0.4, b=0.1$.
$\text{C.}$ $a=0.3, b=0.2$.
$\text{D.}$ $a=0.1, b=0.4$.
设随机变量 $X_i \sim\left[\begin{array}{ccc}-1 & 0 & 1 \\ \frac{1}{4} & \frac{1}{2} & \frac{1}{4}\end{array}\right](i=1,2)$ 且满足条件 $P\left\{X_1+X_2=0\right\}=1$, 则 $P\left\{X_1=X_2\right\}$ 等于
$\text{A.}$ 0 .
$\text{B.}$ $\frac{1}{4}$.
$\text{C.}$ $\frac{1}{2}$.
$\text{D.}$ 1 .
设随机变量 $X$ 与 $Y$ 相互独立, 且都服从区间 $(0,1)$ 上的均匀分布, 则 $P\left\{X^2+Y^2\right.$ $\leqslant 1\}=$
$\text{A.}$ $\frac{1}{4}$.
$\text{B.}$ $\frac{1}{2}$.
$\text{C.}$ $\frac{\pi}{8}$.
$\text{D.}$ $\frac{\pi}{4}$.
设随机变量 $(X, Y)$ 服从二维正态分布 $N\left(0,0 ; 1,4 ;-\frac{1}{2}\right)$, 下列随机变量中服从标准正态分布且与 $X$ 独立的是
$\text{A.}$ $\frac{\sqrt{5}}{5}(X+Y)$.
$\text{B.}$ $\frac{\sqrt{5}}{5}(X-Y)$.
$\text{C.}$ $\frac{\sqrt{3}}{3}(X+Y)$.
$\text{D.}$ $\frac{\sqrt{3}}{3}(X-Y)$.
设 $X, Y$ 相互独立, 它们的分布函数分别为 $F_X(x), F_Y(y)$, 则 $Z=\min \{X, Y\}$ 的分布函数为
$\text{A.}$ $F_z(z)=F_X(z)$.
$\text{B.}$ $F_Z(z)=F_Y(z)$.
$\text{C.}$ $F_Z(z)=\min \left\{F_X(z), F_Y(z)\right\}$.
$\text{D.}$ $\left.F_Z(z)=1-\left[1-F_X(z)\right] 1-F_Y(z)\right]$.
设相互独立的两随机变量 $X$ 和 $Y$ 均服从 $E(1)$, 则 $P\{1 < \min (X, Y) \leqslant 2\}$ 的值为
$\text{A.}$ $e ^{-1}- e ^{-2}$.
$\text{B.}$ $1- e ^{-1}$.
$\text{C.}$ $1- e ^{-2}$.
$\text{D.}$ $e^{-2}-e^{-4}$.
已知随机变量 $X$ 与 $Y$ 相互独立且都服从正态分布 $N\left(\mu, \frac{1}{2}\right)$, 如果 $P\{X+Y \le 1\}=\frac{1}{2}$, 则 $\mu$ 等于
$\text{A.}$ -1 .
$\text{B.}$ 0 .
$\text{C.}$ $\frac{1}{2}$.
$\text{D.}$ 1 .
设 $X$ 和 $Y$ 相互独立都服从 $[0,1]$ 上的均匀分布, 则服从区间或区域上均匀分布的随机变量是
$\text{A.}$ $(X, Y)$.
$\text{B.}$ $X^2$.
$\text{C.}$ $X-Y$.
$\text{D.}$ $X+Y$.
设随机变量 $X$ 和 $Y$ 的联合概率密度为 $f(x, y)=\left\{\begin{array}{ll} e ^{-(x+y)}, & x>0, y>0, \\ 0, & \text { 其他 }\end{array}\right.$ 则 $Z=\frac{X+Y}{2}$ 的概率密度为
$\text{A.}$ $f_Z(z)= \begin{cases}\frac{1}{2} e ^{-(x+y)}, & x>0, y>0, \\ 0, & \text { 其他. }\end{cases}$
$\text{B.}$ $f_Z(z)= \begin{cases} e ^{-\frac{x+y}{2}}, & x>0, y>0, \\ 0, & \text { 其他. }\end{cases}$
$\text{C.}$ $f_Z(z)= \begin{cases}4 z e ^{-2 z}, & z>0, \\ 0, & z \leqslant 0 .\end{cases}$
$\text{D.}$ $f_z(z)= \begin{cases}\frac{1}{2} e ^{-z}, & z>0, \\ 0, & z \neq 0 .\end{cases}$
假设随机变量 $X$ 与 $Y$ 相互独立且都服从参数为 $\lambda$ 的指数分布, 则下列变量中服从参数为 $2 \lambda$ 的指数分布的是
$\text{A.}$ $X+Y$.
$\text{B.}$ $X-Y$.
$\text{C.}$ $\max (X, Y)$.
$\text{D.}$ $\min (X, Y)$.
设随机变量 $X$ 与 $Y$ 相互独立, 且 $X$ 服从标准正态分布 $N(0,1), Y$ 的概率分布为 $P\{Y=0\}=P\{Y=1\}=\frac{1}{2}$, 记 $F_Z(z)$ 为随机变量 $Z=X Y$ 的分布函数, 则函数 $F_Z(z)$ 的间断点个数为
$\text{A.}$ 0 .
$\text{B.}$ 1 .
$\text{C.}$ 2 .
$\text{D.}$ 3 .