一、单选题 (共 8 题 ),每题只有一个选项正确
1. 若 $\sin \alpha=\frac{1}{3}$, 则 $\cos 2 \alpha=$
$\text{A.}$ $\frac{8}{9}$
$\text{B.}$ $\frac{7}{9}$
$\text{C.}$ $-\frac{7}{9}$
$\text{D.}$ $-\frac{8}{9}$
2. 在复平面内, 复数 $z$ 与 $\frac{2}{1-i}$ 对应的点关于实轴对称, 则 $z$ 等于
$\text{A.}$ $1+i$
$\text{B.}$ $-1-i$
$\text{C.}$ $-1+i$
$\text{D.}$ $1-{i}$
3. 设 $\vec{a}, \vec{b}$ 是非零向量, “ $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$ ” 是 “ $\vec{a} / / \vec{b}$ ” 的
$\text{A.}$ 充分而不必要条件
$\text{B.}$ 必要而不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
4. 已知正 $\triangle A B C$ 的边长为 $a$, 那么 $\triangle A B C$ 的平面直观图 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 的面积为
$\text{A.}$ $\frac{\sqrt{3}}{4} a^2$
$\text{B.}$ $\frac{\sqrt{3}}{8} a^2$
$\text{C.}$ $\frac{\sqrt{6}}{8} a^2$
$\text{D.}$ $\frac{\sqrt{6}}{16} a^2$
5. $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 若 $\frac{c}{b} < $ $\cos A$, 则 $\triangle A B C$ 为
$\text{A.}$ 钝角三角形
$\text{B.}$ 直角三角形
$\text{C.}$ 锐角三角形
$\text{D.}$ 等边三角形
6. 如图,测量河对岸的塔高 $A B$ 时可以选与塔底 $B$ 在同一水平面内的两个测点 $C$ 与 $D$, 测得 $\angle B C D=15^{\circ}, \angle B D C=30^{\circ}, C D=30$, 并在点 $C$ 测得塔顶 $A$ 的仰角为 $60^{\circ}$, 则塔高 $A B$ 等于

$\text{A.}$ $5 \sqrt{6}$
$\text{B.}$ $15 \sqrt{3}$
$\text{C.}$ $15 \sqrt{6}$
$\text{D.}$ $5 \sqrt{2}$
7. $\frac{\sqrt{3}}{\cos 190^{\circ}}+\frac{1}{\cos 80^{\circ}}=$
$\text{A.}$ -4
$\text{B.}$ 4
$\text{C.}$ -2
$\text{D.}$ 2
8. $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $b^2+c^2-$ $\sqrt{3} b c=a^2, b c=\sqrt{3} a^2$, 则角 $C$ 的大小是
$\text{A.}$ $\frac{\pi}{6}$ 或 $\frac{2 \pi}{3}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{\pi}{6}$
二、多选题 (共 4 题 ),每题有多个选项正确
9. 下列命题正确的是
$\text{A.}$ 圆锥的顶点与底面圆周上任意一点的连线都是母线
$\text{B.}$ 两个面平行且相似,其余各面都是梯形的多面体是棱台
$\text{C.}$ 以直角梯形的一条直角腰所在的直线为旋转轴, 其余三边旋转一周形成的面所围成的旋转体是圆台
$\text{D.}$ 用平面截圆柱得到的截面只能是圆和矩形
10. $\mathrm{i}$ 为虚数单位, 复数 $z=\frac{3+2 i}{2-i}$, 则为真命题的是
$\text{A.}$ $z$ 在复平面内对应的点在第一象限
$\text{B.}$ $z$ 的虚部是 $-\frac{7}{5}$
$\text{C.}$ $|z|=3 \sqrt{5}$
$\text{D.}$ 若复数 $z_1$ 满足 $\left|z_1-z\right|=1$, 则 $\left|z_1\right|$ 的最大值为 $1+\frac{\sqrt{65}}{5}$
11. 如图所示, 设 $O x, O y$ 是平面内相交成 $\theta\left(\theta \neq \frac{\pi}{2}\right)$ 角的两条数轴, $\overrightarrow{\mathrm{e}}_1, \overrightarrow{\mathrm{e}}_2$ 分别是与 $x$ 轴, $y$ 轴正方向同向的单位向量, 则称平面坐标系 $x O y$ 为 $\theta$ 反射坐标系. 在 $\theta$ 反射坐标系中, 若 $\overrightarrow{O M}=x \overrightarrow{\mathrm{e}_1}+y \overrightarrow{\mathrm{e}_2}$, 则把有序数对 $(x, y)$ 称为向量 $\overrightarrow{O M}$ 的反射坐标, 记为 $\overrightarrow{O M}=(x, y)$. 在 $\theta=\frac{2 \pi}{3}$ 的反射坐标系中, $\vec{a}=(1,2), \vec{b}=(2,-1)$, 其中正确的是
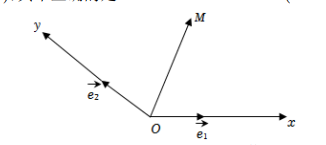
$\text{A.}$ $\vec{a}-\vec{b}=(-1,3)$
$\text{B.}$ $|\vec{a}|=\sqrt{5}$
$\text{C.}$ $\vec{a} \perp \vec{b}$
$\text{D.}$ $|\vec{b}|=\sqrt{7}$
12. 已知 函 数 $ f(x)=\sin \left(\frac{5 \pi}{6}-2 x\right)-2 \sin \left(x-\frac{\pi}{4}\right) \cos \left(x+\frac{3 \pi}{4}\right)$, 则下列关于函数 $f(x)$ 的描述, 正确的是
$\text{A.}$ $f(x)$ 在区间 $\left[0, \frac{\pi}{3}\right]$ 上单调递增
$\text{B.}$ $f(x)$ 图象的一条对称轴是 $x=-\frac{\pi}{6}$
$\text{C.}$ $f(x)$ 图象的一个对称中心是 $\left(\frac{\pi}{3}, 0\right)$
$\text{D.}$ 将 $f(x)$ 的图象向右平移 $\frac{\pi}{3}$ 个单位长度后, 所得的函数图象关于 $y$ 轴对称
三、填空题 (共 10 题 ),请把答案直接填写在答题纸上
13. 平面向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $45^{\circ}, \vec{a}=(1,1),|\vec{b}|=2$, 则 $\mid 3 \vec{a}+\vec{b}\mid=$
14. 已知 $\sin \alpha=\frac{\sqrt{5}}{5}, \sin (\alpha-\beta)=-\frac{\sqrt{10}}{10}, \alpha, \beta$ 均为锐角, 则 $\beta=$
15. 我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的 “三斜公式”, 设 $\triangle A B C$ 三个内角 $A 、 B 、 C$ 所对的边分别为 $a 、 b 、 c$, 面积为 $S$, 则 “三斜求积” 公式为 $S=\sqrt{\frac{1}{4}\left[a^2 c^2-\left(\frac{a^2+c^2-b^2}{2}\right)^2\right]}$. 若 $a^2 \sin C=$ $4 \sin A,(a+c)^2=12+b^2$, 则用 “三斜求积” 公式求得 $\triangle A B C$ 的面积为
16. 已知在 $\triangle O A B$ 中, $O A=O B=2, A B=2 \sqrt{3}$, 动点 $P$ 位于线段 $A B$ 上, 则当 $\overrightarrow{P A} \cdot \overrightarrow{P O}$ 取最小值时, 向量 $\overrightarrow{P A}$ 与 $\overrightarrow{P O}$ 的夹角的余弦值为
17. 已知复数 $z$ 满足 $\frac{1}{z}=\frac{i}{z+1}$, 求 $|z|$;
(2) 计算 $\left(\frac{1+i}{1-i}\right)^6+\frac{\sqrt{2}+\sqrt{3} i}{\sqrt{3}-\sqrt{2} i}$.
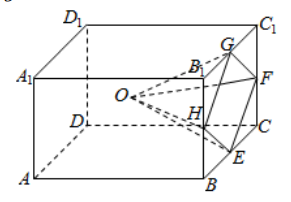
18. 学生到工厂劳动实践, 利用 $3 D$ 打印技术制作模型. 如图,该模型为长方体 $A B C D-A_1 B_1 C_1 D_1$ 挖去四棱锥 $O-E F G H$ 后所得的几何体. 其中 $O$ 为长方体的中心, $E, F, G, H$ 分别为所在棱的中点, $A B=B C=$ $6 \mathrm{~cm}, A A_1=4 \mathrm{~cm} .3 D$ 打印所用原料密度为 $0.9 \mathrm{~g} / \mathrm{cm}^3$, 不考虑打印损耗, 求制作该模型所需原料的质量.
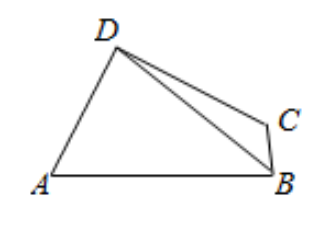
19. 如图, 在四边形 $A B C D$ 中, $\angle D A B=\frac{\pi}{3}, A D: A B=2: 3$, $B D=\sqrt{7}, A B \perp B C$.
(1) 求 $\sin \angle A B D$ 的值;
(2) 若 $\angle B C D=\frac{2 \pi}{3}$, 求 $C D$ 的长.
20. 已知函数 $f(x)=2 \sin ^2 \omega x+2 \sqrt{3} \sin \omega x \cos \omega x-1(\omega>0)$,且函数 $f(x)$ 的最小正周期为 $\pi$.
(1) 求 $f(x)$ 的解析式,并求出 $f(x)$ 的单调递增区间;
(2) 将函数 $f(x)$ 的图象向左平移 $\frac{\pi}{4}$ 个单位长度得到函数 $g(x)$ 的图象, 求函数 $g(x)$ 的最大值及 $g(x)$ 取得最大值时 $x$ 的取值集合.
21. 在① $\frac{\sin A}{\sin B-\sin C}=\frac{b+c}{b-a}$; ②$\frac{c}{a}=\frac{\cos C+1}{\sqrt{3} \sin A}$; ③$2 S=$ $\sqrt{3} \overrightarrow{C A} \cdot \overrightarrow{C B}$ 这三个条件中任选一个, 补充在下面的横线上, 并加以解答.
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别是 $a, b, c, S$ 为 $\triangle A B C$ 的面积, 若 ________ . (填条件序号)
(1) 求角 $C$ 的大小;
(2) 点 $D$ 在 $C A$ 的延长线上, 且 $A$ 为 $C D$ 的中点, 线段 $B D$ 的长度为 2 , 求 $\triangle A B C$ 的面积 $S$ 的最大值.
22. $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $a \sin \frac{A+C}{2}=b \sin A$.
(1) 求 $B$;
(2) 若 $\triangle A B C$ 为锐角三角形, 且 $c=1$, 求 $a$ 的取值范围.