一、单选题 (共 10 题 ),每题只有一个选项正确
1. 2023 的相反数是
2023
-2023
2. 将数 0.0000025 用科学记数法表示为
3. 如图,
是
的直径,
, 则
为

4. 如果从 ,,,,,,,,, 这 10 个数中任意选取一个数,那么取到的数恰好是 5 的倍 数的概率是
5. 已知 ,下列关系式中一定正确的是
6. 如图,
是
的中位线,
平分
交
于
,若
, ,则

7
8
9
10
7. 一组同学一起去种树,如果每人种4棵,还剩下 3 棵树苗;如果每人种 5 棵,则缺少5棵树苗. 设这 组同学有 人,根据题意可列方程为
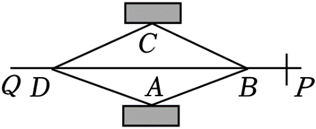
8. 如图是一款汽车干斤顶,其主要部件为四根连杆组成的菱形
和螺旋杆
,当
,
时,
, 两点的距离为
9. 函数 的图象与 轴两个交点的横坐标分别为 , ,且 , , 当 时,该函数的最小值 与 的关系式是
10. 由四个全等的直角三角形和一个小正方形
组成的大正方形
如图所示. 连结
,并 延长交
于点N. 若
,则
的长为

2
3
二、填空题 (共 6 题 ),请把答案直接填写在答题纸上
12. 已知一次函数 与 的图象的交点的坐标是 ,则 , 的方程组 的解为
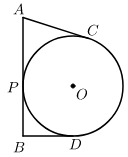
13. 如图,
、、 是
的切线,切点分别为
、、. 若
, ,则
的长 是
14. 已知数据 的方差是 3 , 则一组新数据 的方差是
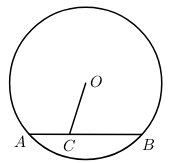
15. 如图所示,小区内有个圆形花坛
,点
在弦
上,
,, ,则这个花 坛的面积为 (结果保留
)
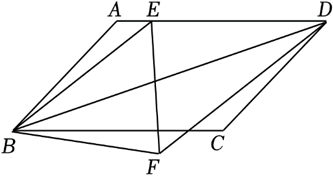
16. 如图,已知在平行四边形
中,
, 点
在
上,
, 将
沿
翻折到
, 连接
, 则
长为 ________ ,
的长为 ________
三、解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
17. 某同学化简分式: 出现了错误,解答过程如下:
解:
(1) 该同学的解答过程是从第
步开始出错.
(2 ) 请写出此题的正确解答过程.
18. 实验学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长进行调查,将抽查 的数据结果进行统计,并绘制两幅不完整的统计图 (A: 不太了解, B: 基本了解, C: 比较了 解,D: 非常了解) . 请根据图中提供的信息回答以下问题:
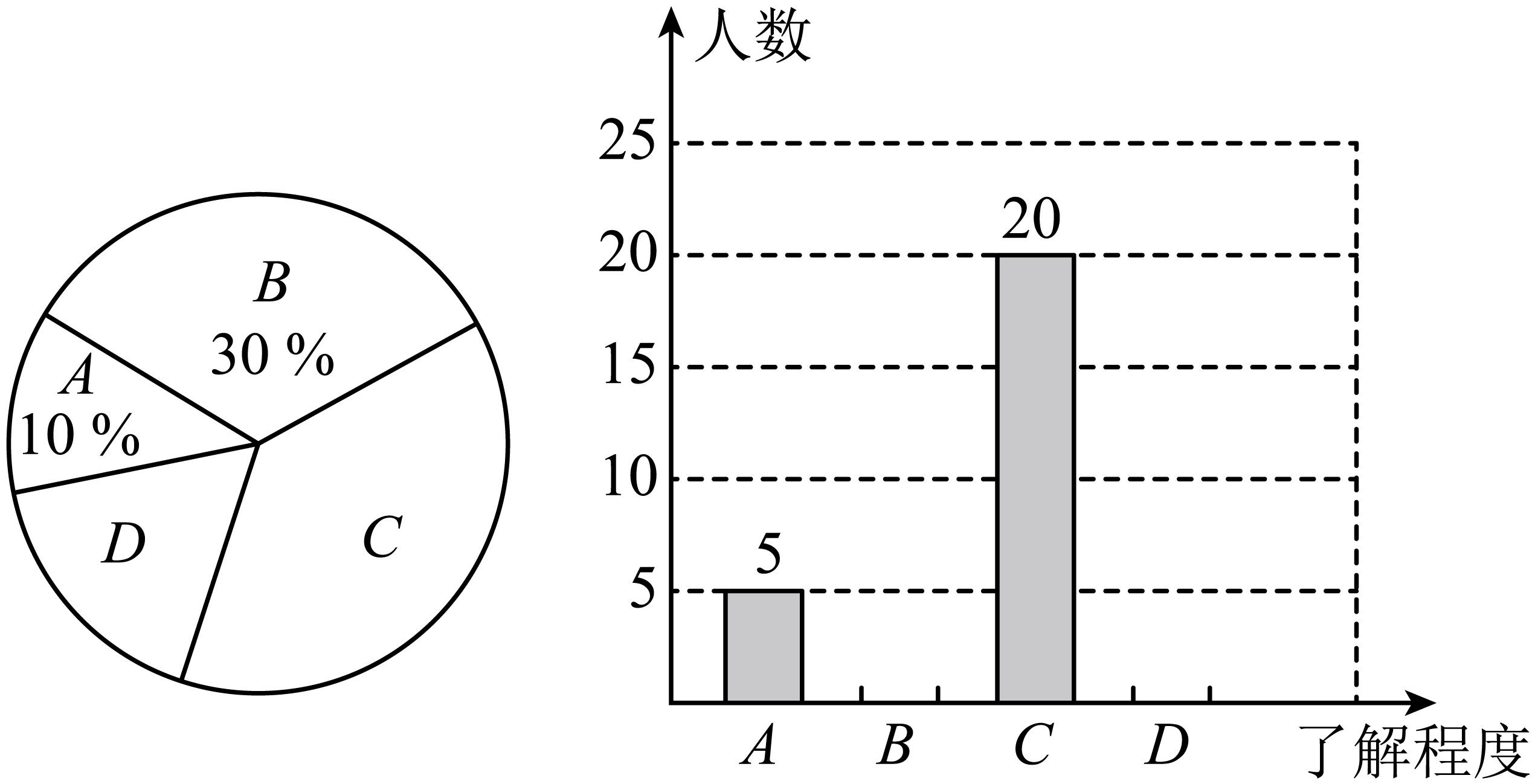
(1)请求出这次被调查的学生家长共有多少人?
(2)请补全条形统计图.
(3)试求出扇形统计图中“比较了解”部分所对应的圆心角度数.
(4)该学校共有2400名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长大约有多 少?
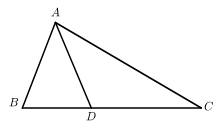
19. 如图,在
中,
为
上一点,
.
(1) 求证:
.
(2) 若
, ,求
的长.
20. 如图,在平面直角坐标系中,直线
与反比例函数
的图象交于
, 两点,已 知
点的纵坐标是 2 .
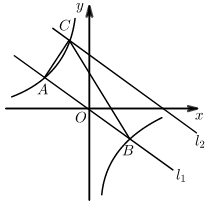
(1)求反比例函数的表达式.
(2) 根据图象直接写出
的解集.
21. 如图,平行四边形
中,
与 相交于点
, 点
为
中点,
交
于点
, 连结
,
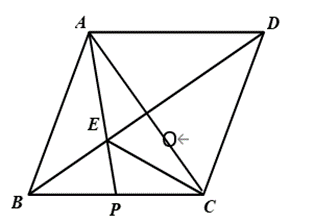
(1) 求证:平行四边形
为菱形;
(2) 若
,
(1)求
的值.
(2)求
的长.
22. 在平面直角坐标系中,二次函数 的图象过点 .
(1) 求该二次函数的解析式;
(2)当 时,求 的最大值与最小值的差;
( 3 ) 若一次函数 的图象与二次函数 的图象交点的横坐标 分别为 和 , 且 , 求 的取值范围.
23. 如图1,已知
为
的直径,点
为
的中点,点
在
上,连接
、、、 、
与
相交于点
.
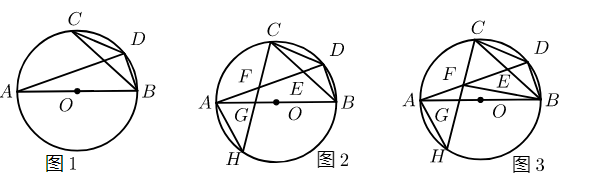
(1) 求证:
.
(2) 如图 2 ,过点
作
的垂线,分别与
,, 相交于点
、、 ,求证:
.
(3) 如图3,在 (2) 的条件下,连接
,若
,求
.