单选题 (共 10 题 ),每题只有一个选项正确
《九章算术》中有一题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:今有大容器5个,小容器1个,总容量为3斛(斛 古代容量单位);大容器1个,小容器5个,总容量为2斛,问大容器、小容器的容量各是多少斛?设大容器的容量为 斛,小容器的容量为 斛,则可列方程组是
$\text{A.}$ $\left\{\begin{array}{l}x+5 y=3 \\ 5 x+y=2\end{array}\right.$
$\text{B.}$ $\left\{\begin{array}{l}5 x+y=3 \\ x+5 y=2\end{array}\right.$
$\text{C.}$ $\left\{\begin{array}{l}5 x=y+3 \\ x=5 y+2\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}5 x=y+2 \\ x=5 y+3\end{array}\right.$
计算 $2-3$ 的结果是
$\text{A.}$ -1
$\text{B.}$ -3
$\text{C.}$ 1
$\text{D.}$ 3
据报道, 2023 年"五一"假期全国国内旅游出游合计 274000000 人次. 数字 274000000 用科学记数法表示是
$\text{A.}$ $27.4 \times 10^7$
$\text{B.}$ $2.74 \times 10^8$
$\text{C.}$ $0.274 \times 10^9$
$\text{D.}$ $2.74 \times 10^9$
下列计算正确的是
$\text{A.}$ $a^6 \div a^2=a^3$
$\text{B.}$ $\left(-a^2\right)^5=-a^7$
$\text{C.}$ $(a+1)(a-1)=a^2-1$
$\text{D.}$ $(a+1)^2=a^2+1$
在一个不透明的袋子里装有 2 个红球和 5 个白球, 它们除颜色外都相同,从中任意摸出 1 个球,则摸出的球为红球的概率是
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{2}{7}$
$\text{D.}$ $\frac{5}{7}$
在平面直角坐标系中, 将点 $(m, n)$ 先向右平移 2 个单位, 再向上平移 1 个单位, 最后所得点的坐标是
$\text{A.}$ $(m-2, n-1)$
$\text{B.}$ $(m-2, n+1)$
$\text{C.}$ $(m+2, n-1)$
$\text{D.}$ $(m+2, n+1)$
如图, 在矩形 $A B C D$ 中, $O$ 为对角线 $B D$ 的中点, $\angle A B D=60^{\circ}$, 动点 $E$在线段 $O B$ 上, 动点 $F$ 在线段 $O D$ 上, 点 $E, F$ 同时从点 $O$ 出发, 分别向终点 $B$, $D$ 运动, 且始终保持 $O E=O F$. 点 $E$ 关于 $A D, A B$ 的对称点为 $E_1, E_2$; 点 $F$ 关于 $B C, C D$ 的对称点为 $F_1, F_2$ 在整个过程中, 四边形 $E_1 E_2 F_1 F_2$ 形状的变化依次是
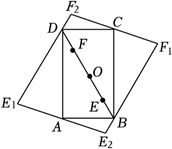
$\text{A.}$ 菱形$\rightarrow$平行四边形$\rightarrow$矩形 $\rightarrow$平行四边形$\rightarrow$菱形
$\text{B.}$ 菱形$\rightarrow$正方形$\rightarrow$平行四边形$\rightarrow$菱形$\rightarrow$平行四边形
$\text{C.}$ 平行四边形$\rightarrow$矩形$\rightarrow$平行四边形$\rightarrow$菱形$\rightarrow$平行四边形
$\text{D.}$ 平行四边形$\rightarrow$菱形$\rightarrow$正方形$\rightarrow$平行四边形$\rightarrow$菱形
已知点 $M(-4, a-2), N(-2, a), P(2, a)$ 在同一个函数图象上, 则这个函数图象可能是
$\text{A.}$ 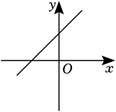 $\text{B.}$
$\text{B.}$ 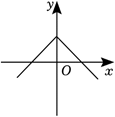 $\text{C.}$
$\text{C.}$ 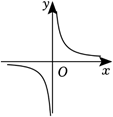 $\text{D.}$
$\text{D.}$ 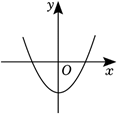
如图, 在 $\triangle A B C$ 中, $D$ 是边 $B C$ 上的点 (不与点 $B, C$ 重合). 过点 $D$作 $D E / / A B$ 交 $A C$ 于点 $E$; 过点 $D$ 作 $D F / / A C$ 交 $A B$ 于点 $F 、 N$ 是线段 $B F$ 上的点, $B N=2 N F: M$ 是线段 $D E$ 上的点, $D M=2 M E$. 若已知 $\triangle C M N$ 的面积, 则一定能求出
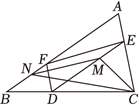
$\text{A.}$ $\triangle A F E$ 的面积
$\text{B.}$ $\triangle B D F$ 的面积
$\text{C.}$ $\triangle B C N$ 的面积
$\text{D.}$ $\triangle D C E$ 的面积
填空题 (共 1 题 ),请把答案直接填写在答题纸上
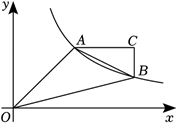
如图, 在平面直角坐标系 $x O y$ 中, 函数 $y=\frac{k}{x}(k$ 为大于 0 的常数, $x>0)$图象上的两点 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$, 满足 $x_2=2 x_1, \triangle A B C$ 的边 $A C / / x$ 轴, 边 $B C / / y$轴, 若 $\triangle O A B$ 的面积为 6, 则 $\triangle A B C$ 的面积是
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知二次函数 $y=-x^2+b x+c$.
(1) 当 $b=4, c=3$ 时,
① 求该函数图象的顶点坐标;
② 当 $-1 \leqslant x \leqslant 3$ 时, 求 $y$ 的取值范围;
(2) 当 $x \leqslant 0$ 时, $y$ 的最大值为 2 ; 当 $x>0$ 时, $y$ 的最大值为 3 ,求二次函数的表达式.
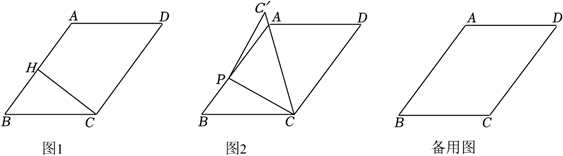
在平行四边形 $A B C D$ 中 (顶点 $A, B, C, D$ 按逆时针方向排列), $A B=12, A D=10, \angle B$ 为锐角, 且 $\sin B=\frac{4}{5}$.
(1) 如图 1, 求 $A B$ 边上的高 $C H$ 的长;
(2) $P$ 是边 $A B$ 上的一动点, 点 $C, D$ 同时绕点 $P$ 按逆时针方向旋转 $90^{\circ}$ 得点 $C^{\prime}$, $D^{\prime}$,
① 如图 2, 当 $C^{\prime}$ 落在射线 $C A$ 上时, 求 $B P$ 的长;
② 当 $\triangle A C^{\prime} D^{\prime}$ 是直角三角形时, 求 $B P$ 的长.