科数网
题号:17161    题型:单选题    来源:2023年浙江省绍兴市中考数学试卷
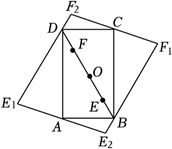
如图, 在矩形 ABCD 中, O 为对角线 BD 的中点, ∠ABD=60∘, 动点 E在线段 OB 上, 动点 F 在线段 OD 上, 点 E,F 同时从点 O 出发, 分别向终点 B, D 运动, 且始终保持 OE=OF. 点 E 关于 AD,AB 的对称点为 E1,E2; 点 F 关于 BC,CD 的对称点为 F1,F2 在整个过程中, 四边形 E1E2F1F2 形状的变化依次是
A. 菱形→平行四边形→矩形 →平行四边形→菱形 B. 菱形→正方形→平行四边形→菱形→平行四边形 C. 平行四边形→矩形→平行四边形→菱形→平行四边形 D. 平行四边形→菱形→正方形→平行四边形→菱形
答案与解析：
答案仅限会员可见 微信内自动登录 或 手机登录 或 微信扫码注册登录 点击我要 开通VIP