单选题 (共 7 题 ),每题只有一个选项正确
我国 “华龙一号” 核电工程采用了世界最高安全要求和最新技术标准。关于核反应堆, 下列说法正确的是
$\text{A.}$ 华龙一号核反应堆是利用可控的核聚变释放核能的
$\text{B.}$ ${ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \rightarrow{ }_{56}^{144} \mathrm{Ba}+{ }_{36}^{89} \mathrm{Kr}+3{ }_0^1 \mathrm{n}$ 是核反应堆的一种典型核反应方程
$\text{C.}$ 中等质量的原子核的比结合能最小,所以核裂变和核聚变都能释放核能
$\text{D.}$ 将控制棒插入铀棒之间深一些, 可多吸收铀核, 链式反应速度会慢一些
2023 年 10 月, 南阳一荆门一长沙特高压交流线路工程全线竣工。在输送功率一定时, 分别用 1000 千伏和 500 千伏对同一段线路输电。下列说法正确的是
$\text{A.}$ 高压输电线输送电流之比为 $2: 1$
$\text{B.}$ 高压输电线路电阻损耗功率之比 $1: 4$
$\text{C.}$ 输电线路上电压损失之比为 $1: 4$
$\text{D.}$ 用户得到的功率之比为 $1: 2$
如图为隐形战机的有源对消电子设备发出与对方雷达发射波匹配的行波, 使对方雷达接受不到反射波, 从而达到雷达隐形的效果。下列说法正确的是
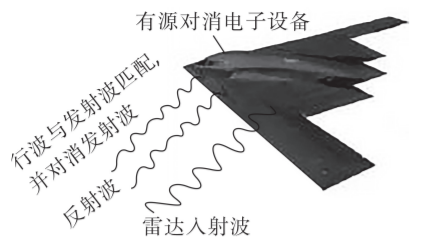
$\text{A.}$ 隐形战机雷达隐形的原理是波的干涉
$\text{B.}$ 隐形战机雷达隐形的原理是波的衍射
$\text{C.}$ 隐形战机雷达隐形的原理是多普勒效应
$\text{D.}$ 行波与对方雷达发射波的频率相同、相位相同
光总是走时间最短的路径。我们在生活中如果也类比光的传播路径行动, 会最快到达目的地。如图甲, 你以恒定的速率从 $A$ 点到 $B$ 过程中需要到河边取一下水, 则类比光的反射路径时间最短。如图乙, 小明在海滩上 $A$ 处发现小张在海中 $B$ 处呼救,已知小明在海滩上奔跑的速度为 $v_1$, 在海水里游泳的速度为 $v_2, v_1>v_2$, 那么小明应该沿图乙中哪条路线去救人用时最短
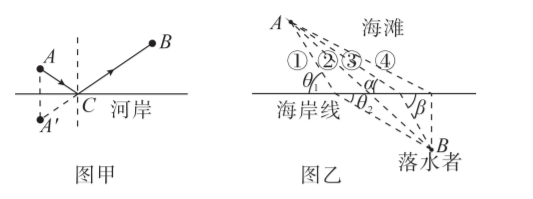
$\text{A.}$ 沿路线 (1), $\frac{\sin \theta_1}{\sin \theta_2}=\frac{v_1}{v_2}, \theta_1 、 \theta_2$ 分别为路线与海岸线的夹角
$\text{B.}$ 沿路线 (2), 沿 $\mathrm{AB}$ 连线方向直线前进, 总路程最短
$\text{C.}$ 沿路线 (3), $\frac{\cos \alpha}{\cos \beta}=\frac{v_1}{v_2}, \alpha 、 \beta$ 分别为路线与海岸线的夹角
$\text{D.}$ 沿路线 (4), 先到最接近 $B$ 的海边, 再垂直海岸到 $B$, 海水中路程最短
某体育老师正在进行投篮教学。某次投篮时, 篮球运动的最高点比篮筐高 $h_1=0.2 \mathrm{~m}$, 且以 $45^{\circ}$ 角落人篮筐中心。若该次投球点比篮筐低 $h_2=0.6 \mathrm{~m}$, 篮球出手的速度大小为 $v$, 方向与水平面的夹角为 $\theta$, 投球点到篮筐中心的水平距离 $x$ 。不计空气阻力, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 下列说法正确的是
$\text{A.}$ $v=4 \mathrm{~m} / \mathrm{s}, \theta=60^{\circ}$
$\text{B.}$ $v=4 \mathrm{~m} / \mathrm{s}, \tan \theta=2$
$\text{C.}$ $x=0.8 \mathrm{~m}$
$\text{D.}$ $x=1.2 \mathrm{~m}$
如图 (a) 为一列简谐横波在 $\mathrm{t}=0.5 \mathrm{~s}$ 时刻的波形图,介质中的两个质点 $P 、 Q$ 此刻离开平衡位置的位移分别为 $0.5 \mathrm{~A} 、-0.5 \mathrm{~A}$, 图 (b) 是质点 $Q$ 的振动图像. 下列说法正确的是
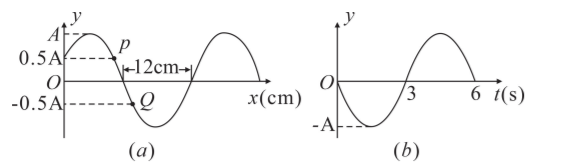
$\text{A.}$ 波沿 $+x$ 方向传播, $0.5 \mathrm{~s}$ 时刻 $P$ 质点正在向 $-y$ 方向振动
$\text{B.}$ 波沿 $-x$ 方向传播, $0.5 \mathrm{~s}$ 时刻 $P$ 质点正在向 $+y$ 方向振动
$\text{C.}$ 波速为 $2 \mathrm{~cm} / \mathrm{s}, P 、 Q$ 振动方向有时相同有时相反
$\text{D.}$ 波速为 $4 \mathrm{~cm} / \mathrm{s}, 0.5 \mathrm{~s}$ 时刻质点 $P$ 在加速、质点 $Q$ 在减速
新时代的中国北斗导航系统是世界一流的。空间段由若干地球静止轨道卫星、倾斜地球同步轨道卫星和中圆地球轨道卫星组成。已知地球表面两极处的重力加速度为 $g_0$, 赤道列说法正确的是
$\text{A.}$ 北斗地球同步卫星距离地球表面的高度 $h=\left(\sqrt[3]{\frac{g_1}{g_0-g_1}}-1\right) R$
$\text{B.}$ 北斗地球同步卫星距离地球表面的高度 $h=\left(\sqrt[3]{\frac{g_0}{g_0-g_1}}-1\right) R$
$\text{C.}$ 地球的平均密度 $\rho=\frac{3 g_1}{4 \pi G R}$
$\text{D.}$ 地球的近地卫星的周期 $T_0=2 \pi \sqrt{\frac{R}{g_1}}$
多选题 (共 4 题 ),每题有多个选项正确
小明查询从武汉到广州的高铁时间时, 发现 G881 比 G883 快 8 分钟, 再查时刻表, 发现 G883 比 G881 中途多停一站。假设这两辆车在出站和进站时均做加速度大小为 $a$ 的匀变速直线运动, 除进站、出站、停留时间以外, 均以恒定的速率 $v=324 \mathrm{~km} / \mathrm{h}$ 匀速运动, 根据列车时刻表, 下列正确的是
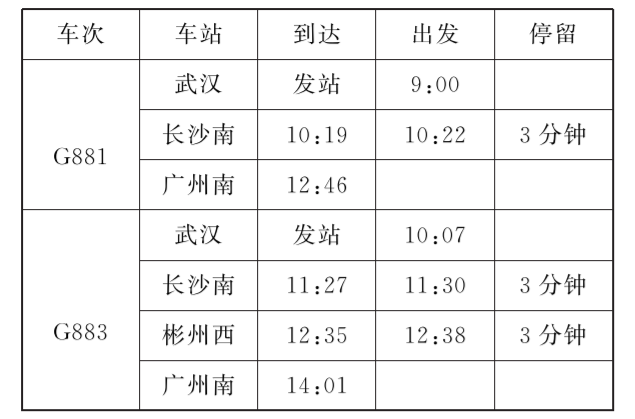
$\text{A.}$ 除掉停车时间, 多出的运行时间是 $\frac{v}{a}$
$\text{B.}$ 除掉停车时间, 多出的运行时间是 $\frac{2 v}{a}$
$\text{C.}$ 列车的加速度为 $0.6 \mathrm{~m} / \mathrm{s}^2$
$\text{D.}$ 列车的加速度为 $0.3 \mathrm{~m} / \mathrm{s}^2$
如图所示, 水平向右的匀强电场中有 $O A 、 O B$ 两个挡板, 分别与坚直方向夹角为 $\alpha_1=30^{\circ}$ 和 $\alpha_2=60^{\circ}$, 正电子、负电子和质子从 $O$ 点竖直向下以相同的初速度 $v_0$ 射人电场, 三种粒子都打在板上被吸收, 只考虑匀强电场给电荷的电场力, 不计其它相互作用力, 则

$\text{A.}$ 正电子和质子打在板上时速度方向相同
$\text{B.}$ 正、负电子的运动时间比为 $1: 3$
$\text{C.}$ 正、负电子电势能的减少量之比为 $1: 9$
$\text{D.}$ 质子打在板上的位置比正电子落点的电势高
如图, 质量为 $M$ 的光滑 $T$ 型金属框 $Q$ 置于水平绝缘平台上, 组成 $Q$ 的几条金属导轨中, $A_1 A$ 与 $B_1 B$ 为足够长的间距为 $L$ 的平行导轨, $E F$ 长为 $2 L$ 且与 $A_1 A$ 垂直。整个装置始终处于坚直向下的匀强磁场中 (未画出), 磁感应强度大小为 $B$, 质量为 $m$ 的导体棒 $P$ 在导轨间的电阻为 $r$, 与平行导轨保持垂直且良好接触。不计金属框的电阻,下列说法正确的是
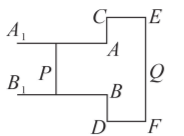
$\text{A.}$ 用水平恒力 $F$ 向右拉金属框 $Q$, 足够长时间后 $P$ 棒的加速度恒定, 最终回路磁通量不变
$\text{B.}$ 若金属框 $Q$ 固定不动, 给 $P$ 一个初速度 $v_0$,则 $P$ 的速度会随位移均匀减小
$\text{C.}$ 若棒 $P$ 固定, 使框 $Q$ 以速度 $v$ 匀速向右运动时, $Q$ 产生的感应电动势为 $2 B L v$
$\text{D.}$ 若 $P 、 Q$ 不固定, 给棒 $P$ 水平向右的初速度 $v_0$, 则流过 $\mathrm{P}$ 的总电量为 $\frac{M m v_0}{(M+m) B L}$
某人最多能提起质量为 $m$ 的物体, 如图, 现在他在机场要把质量为 $M$ 的行李箱通过倾角为 $\alpha$ 的斜坡 $A B$ 拉上水平平台 $B C$, 已知行李箱与 $A B C$ 路面的动摩擦因数均为 $\tan \beta$,重力加速度为 $g,(\alpha+\beta) < 90^{\circ}$, 下列说法正确的是
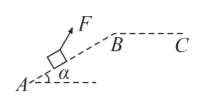
$\text{A.}$ 在斜坡 $A B$ 上,此人最多能匀速拉动质量为 $\frac{m}{\sin (\alpha+\beta)}$ 的物体
$\text{B.}$ 拉力 $F$ 与斜坡的夹角为 $(\alpha+\beta)$ 时最省力
$\text{C.}$ 若水平面上匀速拉物体, 拉力 $F$ 由水平变到坚直方向过程中, $F$ 的功率先减小后增大
$\text{D.}$ 在水平面上想要以最大加速度加速, 拉力 $F$ 应与水平面成 $\beta$ 角斜向上拉
填空题 (共 2 题 ),请把答案直接填写在答题纸上
某科技小组想验证匀速圆周运动向心力大小的表达式 $F_n=m \omega^2 r$, 装置如图, 用能够显示并调节转动频率的小电动机带动坚直轴匀速转动, $O B$ 为坚直轴的中心线, 长为 $d$ 的水平横臂 $O A$ 固定在 $O B$ 上, 不可伸长的轻细线上端固定在 $A$ 处, 下端穿过球心并固定。在装置后面放一贴有白纸的坚直平板, 调节装置使初位置 $O A 、 O B$ 所在的平面与竖直平板平行, 用平行光源将装置垂直投影在坚直板的白纸上。
(1) 描下装置在白纸上的投影 $O B$ 和 $O A$ 。测出 $O A$ 投影长度也为 $d$, 说明平行光源与墙垂直。(2) 启动电动机, 记录电动机的转动频率 $f$, 当小球转动稳定时, 利用直尺与影子相切, 描下小球轨迹在白纸上影子的最下边缘水平切线 $C B$, 记下小球到达最右边缘影子的坚直切线 $C C_1, C B$ 与 $C C_1$ 交于 $C$ 点, $B$ 为 $C B$ 与 $O B$ 的交点。
(3)关闭电动机, 改变电动机的转动频率, 重复上述实验.
(1) 已知当地的重力加速度为 $g$, 测出了小球的直径 $D$ 。为验证向心力公式, 还需测量选项中描述的物理量即可。(从下列四个选项中选择一个)
A. 小球的质量 $m$
B. $O B$ 高度差 $h$
C. $A C$ 绳长 $L$
D. 画出 $C A$ 延长线与 $B O$ 延长线的交点 $E$, 测 $E B$ 的距离 $H$
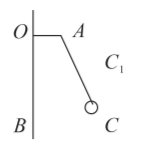
(2)丙同学作出 (1)中正确选择的物理量随 (选填 “ $\frac{1}{f}$ ”或 “ $\frac{1}{f^2}$ ”) 变化的图像为一直线, 但不过原点。如果图像纵轴截距为 , 斜率为 , 则可验证向心力公式 $F_n=m \omega^2 r$ 成立。(用第一问已知或所测的量表示)
某同学想测如图 (1) 集成电路里很薄的方块电阻 $R_0$ 的电阻率 $\rho$, 同时测干电池的电动势 $E$ 和内阻 $r$, 他设计了如图 (2) 的电路。已知方块电阻的上、下表面是边长为 $L$ 的正方形,上下表面间的厚度为 $d$,连人电路时电流方向如图 (1)。
(1) 断开开关 $k$, 闭合开关 $S$, 改变电阻箱 $R$ 阻值, 记录不同 $R$ 对应的电压表的示数 $U$;
(2) 将开关 $S 、 k$ 均闭合, 改变电阻箱 $R$ 阻值, 再记录不同 $R$ 对应的电压表的示数 $U$;
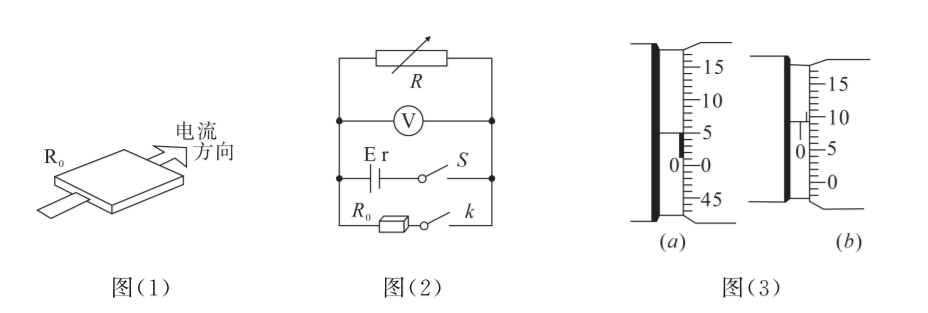
(1)画出步骤(1)(2)记录的数据对应的 $\frac{1}{U}$ 随 $\frac{1}{R}$ 变化关系的图像分别对应如图 (4)的两条图线, 横截距分别为 $-a_1 、-a_2$, 纵截距为 $b_1 、 b_2$, 请判断哪条是步骤(1)对应的图线, 则电源的电动势 $E=$ , 电源内阻 $r=$ , 则方块电阻 $R_0=$
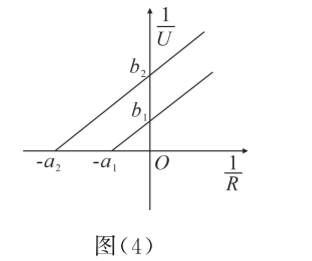
(2)若考虑电压表内阻的影响,方块电阻的测量值 (选填"偏大"、"偏小"、"不变")。
(3) 要测出方块电阻的电阻率, 先用螺旋测微器测量上下表面间的厚度 $d$ 。在测微螺杆和测砧相接时, 示数如图 (a)。在夹方块电阻测厚度时示数如图 $(b)$, 则厚度 $d=$ $\mathrm{mm}$ 。
(4) 方块电阻的电阻率表达式为 $\rho=$。(用 $a 、 b 、 c 、 d$ 等已测量字母表示)
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
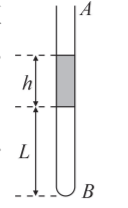
如图所示, 一根一端封闭粗细均匀足够长的细玻璃管 $A B$ 开口向上坚直放置, 管内用高 $h=15 \mathrm{~cm}$ 的水银柱封闭了一段长 $L=31 \mathrm{~cm}$ 的空气柱。已知外界大气压强为 $p_0=75 \mathrm{cmHg}$, 封闭气体的温度为 $T_1=310 \mathrm{~K} 。 g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 则 (1)封闭气体温度 $T_1$ 不变, 试管以 $2 \mathrm{~m} / \mathrm{s}^2$ 的加速度坚直向上加速, 求水银柱稳定时试管内空气柱长度;
(2) 缓慢转动玻璃管至管口向下后坚直固定, 同时使封闭气体的温度缓慢降到 $T_3=280 \mathrm{~K}$,求此时试管内空气柱的长度 $L_3$ 。
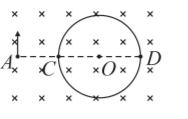
如图, 磁感应强度大小为 $B$ 匀强磁场垂直纸面向里。点 $A 、 C 、 O 、 D$ 处于一条水平线上, 且 $A C=C O=O D=r 。 A$ 处有一个粒子源, 坚直向上同时射出速率不同的同种带电粒子, 粒子经过以 $O$ 为圆心、 $r$ 为半径的圆周上各点。已知粒子质量为 $m$, 电量的绝对值为 $q$, 不计粒子重力和粒子间相互作用力, 问:
(1)粒子带正电荷还是负电荷? 到达 $C$ 和到达 $D$ 处的粒子的速率比 $v_1: v_2$;
(2) 求粒子到达圆周所需的最短时间 $t_{\min }$, 及最先到达圆周的粒子的速度大小 $v_3$ 。
如图所示, 倾角 $\theta=30^{\circ}$ 足够长的光滑斜面固定在水平面上, 两个物体 $A 、 B$ 通过细绳及轻弹簧连接于光滑轻滑轮两侧, $B$ 的质量为 $m$, 开始时用手按住物体 $A$, 物体 $B$静止于地面, 滑轮两边的细绳恰好伸直, 且弹簧处于原长状态。松开手后, 当 $B$ 刚要离开地面时, $A$ 恰达最大速度 $v$,空气阻力不计。

(1) 求 $A$ 的质量 $M$;
(2) 已知弹簧的弹性势能 $E_p$ 与形变量 $x$ 的关系 $E_p=\frac{1}{2} k x^2$, 求弹簧的劲度系数为 $k$;
(3) $A$ 下滑过程中弹簧最长时, $A$ 的速度 $v_1$ 为多少?