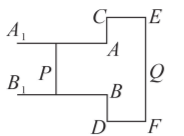
如图, 质量为 $M$ 的光滑 $T$ 型金属框 $Q$ 置于水平绝缘平台上, 组成 $Q$ 的几条金属导轨中, $A_1 A$ 与 $B_1 B$ 为足够长的间距为 $L$ 的平行导轨, $E F$ 长为 $2 L$ 且与 $A_1 A$ 垂直。整个装置始终处于坚直向下的匀强磁场中 (未画出), 磁感应强度大小为 $B$, 质量为 $m$ 的导体棒 $P$ 在导轨间的电阻为 $r$, 与平行导轨保持垂直且良好接触。不计金属框的电阻,下列说法正确的是

A. 用水平恒力 $F$ 向右拉金属框 $Q$, 足够长时间后 $P$ 棒的加速度恒定, 最终回路磁通量不变
B. 若金属框 $Q$ 固定不动, 给 $P$ 一个初速度 $v_0$,则 $P$ 的速度会随位移均匀减小
C. 若棒 $P$ 固定, 使框 $Q$ 以速度 $v$ 匀速向右运动时, $Q$ 产生的感应电动势为 $2 B L v$
D. 若 $P 、 Q$ 不固定, 给棒 $P$ 水平向右的初速度 $v_0$, 则流过 $\mathrm{P}$ 的总电量为 $\frac{M m v_0}{(M+m) B L}$