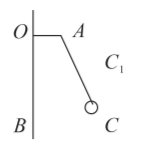
某科技小组想验证匀速圆周运动向心力大小的表达式 $F_n=m \omega^2 r$, 装置如图, 用能够显示并调节转动频率的小电动机带动坚直轴匀速转动, $O B$ 为坚直轴的中心线, 长为 $d$ 的水平横臂 $O A$ 固定在 $O B$ 上, 不可伸长的轻细线上端固定在 $A$ 处, 下端穿过球心并固定。在装置后面放一贴有白纸的坚直平板, 调节装置使初位置 $O A 、 O B$ 所在的平面与竖直平板平行, 用平行光源将装置垂直投影在坚直板的白纸上。
(1) 描下装置在白纸上的投影 $O B$ 和 $O A$ 。测出 $O A$ 投影长度也为 $d$, 说明平行光源与墙垂直。(2) 启动电动机, 记录电动机的转动频率 $f$, 当小球转动稳定时, 利用直尺与影子相切, 描下小球轨迹在白纸上影子的最下边缘水平切线 $C B$, 记下小球到达最右边缘影子的坚直切线 $C C_1, C B$ 与 $C C_1$ 交于 $C$ 点, $B$ 为 $C B$ 与 $O B$ 的交点。
(3)关闭电动机, 改变电动机的转动频率, 重复上述实验.
(1) 已知当地的重力加速度为 $g$, 测出了小球的直径 $D$ 。为验证向心力公式, 还需测量选项中描述的物理量即可。(从下列四个选项中选择一个)
A. 小球的质量 $m$
B. $O B$ 高度差 $h$
C. $A C$ 绳长 $L$
D. 画出 $C A$ 延长线与 $B O$ 延长线的交点 $E$, 测 $E B$ 的距离 $H$
(2)丙同学作出 (1)中正确选择的物理量随 (选填 “ $\frac{1}{f}$ ”或 “ $\frac{1}{f^2}$ ”) 变化的图像为一直线, 但不过原点。如果图像纵轴截距为 , 斜率为 , 则可验证向心力公式 $F_n=m \omega^2 r$ 成立。(用第一问已知或所测的量表示)
(1) 描下装置在白纸上的投影 $O B$ 和 $O A$ 。测出 $O A$ 投影长度也为 $d$, 说明平行光源与墙垂直。(2) 启动电动机, 记录电动机的转动频率 $f$, 当小球转动稳定时, 利用直尺与影子相切, 描下小球轨迹在白纸上影子的最下边缘水平切线 $C B$, 记下小球到达最右边缘影子的坚直切线 $C C_1, C B$ 与 $C C_1$ 交于 $C$ 点, $B$ 为 $C B$ 与 $O B$ 的交点。
(3)关闭电动机, 改变电动机的转动频率, 重复上述实验.
(1) 已知当地的重力加速度为 $g$, 测出了小球的直径 $D$ 。为验证向心力公式, 还需测量选项中描述的物理量即可。(从下列四个选项中选择一个)
A. 小球的质量 $m$
B. $O B$ 高度差 $h$
C. $A C$ 绳长 $L$
D. 画出 $C A$ 延长线与 $B O$ 延长线的交点 $E$, 测 $E B$ 的距离 $H$

(2)丙同学作出 (1)中正确选择的物理量随 (选填 “ $\frac{1}{f}$ ”或 “ $\frac{1}{f^2}$ ”) 变化的图像为一直线, 但不过原点。如果图像纵轴截距为 , 斜率为 , 则可验证向心力公式 $F_n=m \omega^2 r$ 成立。(用第一问已知或所测的量表示)