单选题 (共 9 题 ),每题只有一个选项正确
2023 的相反数是
$\text{A.}$ $\frac{1}{2023}$
$\text{B.}$ $-\frac{1}{2023}$
$\text{C.}$ $ 2023$
$\text{D.}$ $ -2023$
计算 $a^6 \div\left(-a^2\right)$ 的结果是
$\text{A.}$ $a^3$
$\text{B.}$ $a^4$
$\text{C.}$ $-a^3$
$\text{D.}$ $-a^4$
美丽富饶的江汉平原, 文化底蕴深厚, 人才辈出. 据统计, 该地区的天门、仙桃、潜江和江汉油田 2014 年共有约 25000 名初中毕业生参加了毕业生参加统一的学业考试, 将25000用科学记数法可表示为
$\text{A.}$ $25 \times 10^3$
$\text{B.}$ $2.5 \times 10^4$
$\text{C.}$ $2.5 \times 10^5$
$\text{D.}$ $0.25 \times 10^6$
如图, 直线 $a / / b / / c$, 直角三角板的直角顶点落在直线 $b$ 上, 若 $\angle 1=38^{\circ}$, 则 $\angle 2$ 等于
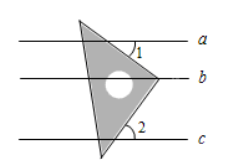
$\text{A.}$ $38^{\circ}$
$\text{B.}$ $42^{\circ}$
$\text{C.}$ $52^{\circ}$
$\text{D.}$ $62^{\circ}$
如图, 下列四个几何体中, 其主视图、左视图、俯视图中只有两个相同的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 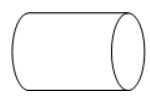
与 $\sqrt{11}$ 最接近的两个整数是
$\text{A.}$ 1 和 2
$\text{B.}$ 2 或 3
$\text{C.}$ 3 和 4
$\text{D.}$ 4 和 5
如图, 电路图上有四个开关 $A 、 B 、 C 、 D$ 和一个小灯泡, 闭合开关 $D$ 或同时闭合开关 $A 、$ $B 、 C$ 都可使小灯泡发光, 则任意闭合其中两个开关, 小灯泡发光的概率是
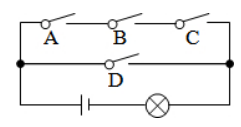
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{6}$
如图, 在 $\triangle A B C$ 中, 以 $B C$ 为直径的圆分别交边 $A C, A B$ 于 $D, E$ 两点, 连接 $B D, D E$. 若 $B D$ 平分 $\angle A B C$, 则下列结论不一定成立的是
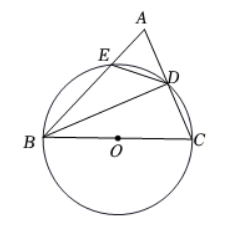
$\text{A.}$ $B D \perp A C$
$\text{B.}$ $A C^2=2 A B \cdot A E$
$\text{C.}$ $\triangle A D E$ 是等腰三角形
$\text{D.}$ $B C=2 A D$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
如图, 已知 $A D / / B C, \angle B=30^{\circ}, D B$ 平分 $\angle A D E$, 则 $\angle D E C=$
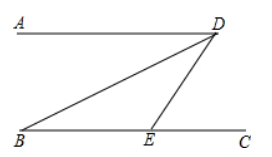
分式方程 $-\frac{2}{x}=\frac{2}{x-1}$ 的解是
在平面直角坐标系中, 已知抛物线 $y_1=a x^2+3 a x-4 a(a$ 是常数, 且 $a < 0)$, 直线 $A B$ 过点 $(0, n)(-5 < n < 5)$ 且 垂直于 $y$ 轴.
(1) 该抛物线顶点的纵坐标为 ( 用含 $a$ 的代数式表示).
(2) 当 $a=-1$ 时, 沿直线 $A B$ 将该抛物线在直线上方的部分翻折, 其余部分不变, 得到新图象 $G$, 图象 $G$ 对应的函数记为 $y_2$, 且当一 $\leq x \leq 2$ 时, 函数 $y_2$ 的最大值与最小值之差小于 7 , 则 $n$ 的取值范围为
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $\tan ^2 45^{\circ}-2 \sin 30^{\circ}+(\sqrt{2}-1)^0-\left(\frac{1}{2}\right)^{-2}$.
如图, 某登山队在山脚 $A$ 处测得山顶 $B$ 处的仰角为 $45^{\circ}$, 沿坡角 $30^{\circ}$ 的斜坡 $A D$ 前进 $1000 \mathrm{~m}$ 后到达 $D$ 处, 又测得山顶 $B$ 处的仰角为 $60^{\circ}$. 求山的高度 $B C$.
观察下面的点阵图和相应的等式, 探究其中的规律:
(1) 认真观察, 并在(4)后面的横线上写出相应的等式.
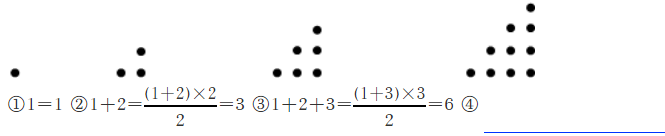
(2) 结合 (1) 观察下列点阵图, 并在(5)后面的横线上写出相应的等式.
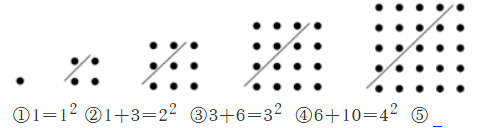
(3) 通过猜想, 写出 (2) 中与第 $n$ 个点阵相对应的等式
如图所示的正方形网格中, $\triangle A B C$ 的顶点均在格点上, 在所给直角坐标系中解 答下列问题:
(1) 分别写出点 $A 、 B$ 两点的坐标并作出 $\triangle A B C$ 以原点为旋转中心逆时针旋转 $180^{\circ}$ 的 $\triangle A_1$ $B_1 C_1$;
( 2 ) 作出点 $C$ 关于 $x$ 轴的对称点 $P$. 若点 $P$ 向右平移 $x$ 个单位长度后落在 $\triangle A_1 B_1 C_1$ 的内部, 请直接写出 $x$ 的取值范围.
如图, $C D$ 为 $\odot O$ 的直径, $C D \perp A B$, 垂足为点 $F, A O \perp B C$, 垂足为 $E, B C=2 \sqrt{3}$,
( 1 ) 求 $A B$ 的长;
(2) 求 $\odot O$ 的半径
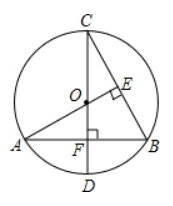
为了了解学生喜爱篮球节目的情况, 在中国篮球职业联赛期间期间, 小明对班级同学一周内收看篮球赛的次数情况 作了调查, 调查结果统计如图所示 ( 其中女生收看3 次的人数没有标出 ). 根据上述信息, 解答下列各题:
(1) 该班级男生人数是 ________ , 男生收看篮球赛次数的中位数是 ________
( 2 ) 对于某个群体, 我们把一周内收看篮球赛次数不低于 3 次的人数占其所在群体总人数的百分比叫做该群体对篮球节目的“关 注指数”. 如果该班级女生对篮球赛的“关注指数”比男生低 $5 \%$, 试求该班级女生人数;
( 3 ) 为进一步分析该班级男、女生收看篮球赛次数的特点, 小明给出了女生的部分统计量 (如表).

根据你所学过的统计知识, 适当计算男生的有关统计量, 进而比较该班级男、女生收看篮球赛次数的波动大小
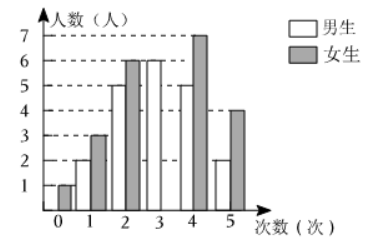
如图, 天娇生态园要建造一圆形喷水池, 在水池中央垂直于水面安装 一个柱子 $O A, O$ 恰在水面中心, $O A$ 高 3 米, 如图 1 , 由柱子顶端处的喷头向外喷水, 水流在各方面沿形状相同的抛物线落下.
(1) 如果要求设计成水流在离 $O A$ 距离为 1 米处达到最高点, 且与水面的距离是 4 米, 那么水池的内部半径至少要多少米, 才能使喷出的水不致落到池外; ( 利用图 2 所示的坐标系进行计算)
(2)若水流喷出的抛物线形状与 (1) 相同, 水池内部的半径为 5 米, 要使水流不落到池外, 此时水流达到的最高点与水面的距离 应是多少米?
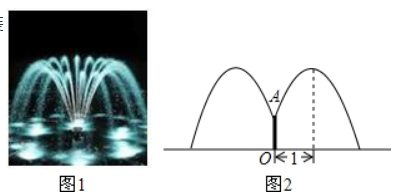
如图1, $D$ 是 $\triangle A B C$ 的 $B C$ 边上的中点, 过点 $D$ 的一条直线交 $A C$ 于 $F$, 交 $B A$ 的延长线于 $E, A G / / B C$ 交 $E F$ 于 $G$, 我们可 以证明 $E G \cdot D C=E D \cdot A G$ 成立(不要求考生证明 ).
(1) 如图 2, 若将图1中的过点 $D$ 的一条直线交 $A C$ 于 $F$, 改为交 $C A$ 的延长线于 $F$, 交 $B A$ 的延长线于 $E$, 改为交 $B A$ 于 $E$, 其它条件不 变, 则 $E G \cdot D C=E D \cdot A G$ 还成立吗? 如果成立, 请给出证明; 如果不成立, 请说出理由;
( 2 ) 根据图 2 , 请你找出 $E G 、 F D 、 E D 、 F G$ 四条线段之间的关系, 并给出证明;
(3) 如图3, 若将图1中的过点 $D$ 的一条直线交 $A C$ 于 $F$, 改为交 $C A$ 的反向延长线于 $F$, 交 $B A$ 的延长线于 $E$, 改为交 $B A$ 于 $E$, 其它条件 不变, 则 ( 2$)$ 得到的结论是否成立?
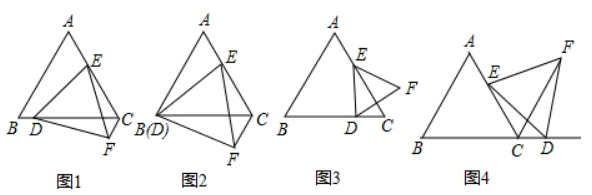
如图1, $\triangle A B C$ 是等边三角形, 点 $E$ 在 $A C$ 边上, 点 $D$ 是 $B C$ 边上的一个动点, 以 $D E$ 为边作等边 $\triangle D E F$, 连接 $C F$.
(1) 当点 $D$ 与点 $B$ 重合时, 如图 2 , 求证: $C E+C F=C D$;
(2) 当点 $D$ 运动到如图 3 的位置时, 猜想 $C E 、 C F 、 C D$ 之间的等量关系, 并说明理由;
(3) 只将条件 “点 $D$ 是 $B C$ 边上的一个动点” 改为 “点 $D$ 是 $B C$ 延长线上的一个动点”, 如图 4 , 猜想 $C E 、 C F 、 C D$ 之间的等量关系为 (不必证明)。