如图, 在 $\triangle A B C$ 中, 以 $B C$ 为直径的圆分别交边 $A C, A B$ 于 $D, E$ 两点, 连接 $B D, D E$. 若 $B D$ 平分 $\angle A B C$, 则下列结论不一定成立的是
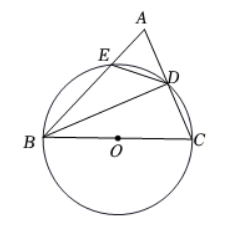

A. $B D \perp A C$
B. $A C^2=2 A B \cdot A E$
C. $\triangle A D E$ 是等腰三角形
D. $B C=2 A D$